Functions

A function is a relation in which each possible input value leads to exactly one output value. We use functions for countless applications because it allows us to describe the relationship between two quantities. This relationship is essential because allows us to describe, analyze, and make predictions.

Relations

A relation is a set of ordered pairs. An example of a relation would be $A = \{(1, -1), (2, -2), (3, -3), (-4, 4), (-5, 5)\}$.

The input values of a function make up the domain and is also known as the independent variable. The input value is often labeled with a $x$ and is the first component of an ordered pair. On the other hand, the output values of a function make up the range and is also known as the dependent variable. The output value is often labeled with a $y$ and is the second component of an ordered pair.

To determine if a relation is a function, we need to verify that every value in the domain leads to only one value in the output. This method also applies to functions in tabular form.

Fig. 1 - Relations as Function

note

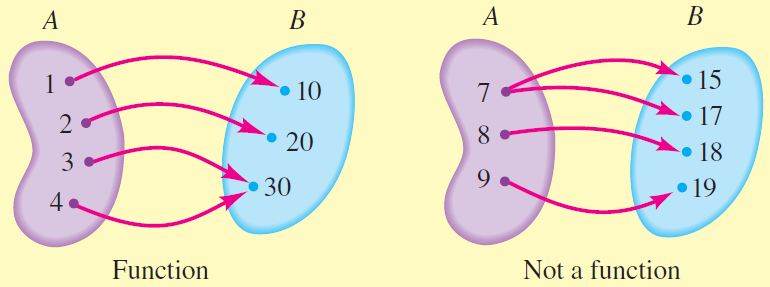
Two different input values can lead to the same output value and would still be a function as long as the each input value leads to only one output value.

Function Notation

The standard function notation is a notation that helps define a function. If $x$ is the independent variable and $y$ is the dependent variable, then using the notation, the function $f$ can be written as $y = f(x)$. We read this as $y$ is a function of $x$ and $f(x)$ can be read as $f$ of $a$.

The notation $f(x)$ shows us that $f$ is depends on $x$ and so we can replace the $x$ with a value to get a result from $f(x)$ through substitution. This also means we can use an algebraic expression as the input in the parenthesis. For example, $f(a + b)$ means first add $a$ and $b$, and the result is the input for the function $f$.

note

The letters $f$, $g$, and $h$ are often used to represent functions just like we use $x$, $y$, and $z$ to represent numbers in mathematics.

Functions in Algebraic Form

A function in algebraic form is expressed as an equation where the function notation is on one side of the equation and the expression on the other side. For example, $f(x) = 2x + 3$ is a function expressed in algebraic form. To evaluate we substitute for the independent variable and simplify to get the result.

We can express a formula in function notation by isolating the the output variable on one side while having the other side as an expression that involves only the input variable. All the algebraic methods used for equations can be used with functions.

$\underline{Example}$

Express the relationship $8n + 4p = 16$ as a function $p = f(n)$, if possible.

$4p = -8n + 16$

$p = -2n + 4$

$p = f(n) = -2n + 4$

One to One Functions

A function can have more than one input value that leads to the same output value. However, a one-to-one function is a function that only has one input value for each output value as well as having only one output value for each input value. For example, letter grades to numerical grades are one to one functions because each input and output are unique.

Vertical and Horizontal Line Test

We often express functions in terms of graphs and all these functions come in different shapes. For example, the function $f(x) = x + 2$ will produce a straight line that intercepts the y-axis at $(0, 2)$.

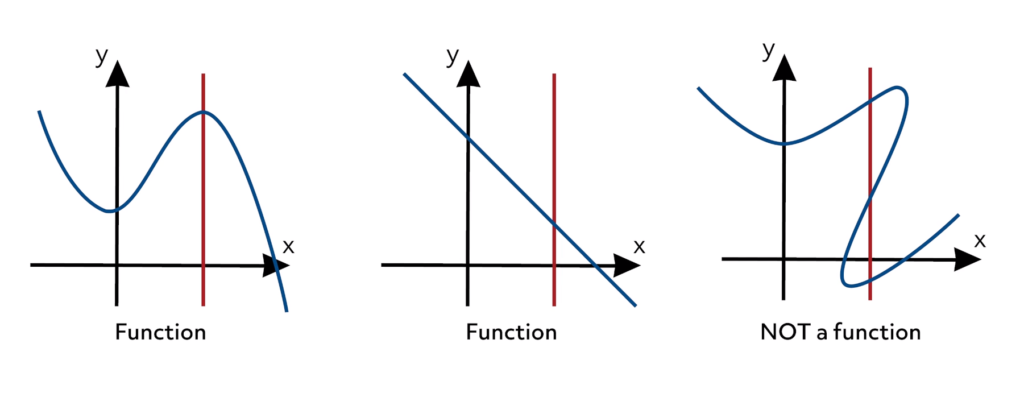
To determine whether a graph represents a function, we can use the vertical line test where we draw any vertical line on the graph and if it intersects the graph more than once than it is not a function because it means one input has more than one output.

Fig. 2 - Vertical Line Test

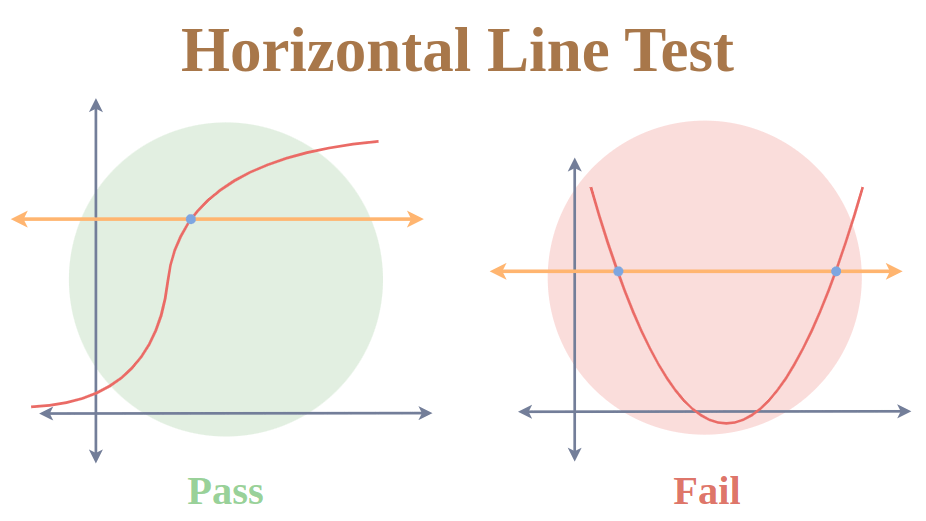
Once a graph has been determined to be a function, we can use the horizontal line test to determine if it is a one-to-one function. We draw horizontal lines through the graph and if any of those lines intersect, then the graph is not an one to one function.

Fig. 3 - Horizontal Line Test

Types of Functions

There are some common functions that we come across often in mathematics and it is useful to know the shape of their graphs, their unique characteristics, and their algebraic formulas. These basic functions are a building block we can use for various other functions.

Name	Function	Graph
Constant	$f(x) = c$ where $c$ is a constant
Identity	$f(x) = x$
Absolute Value	$f(x) = \:\mid x \mid$
Quadratic	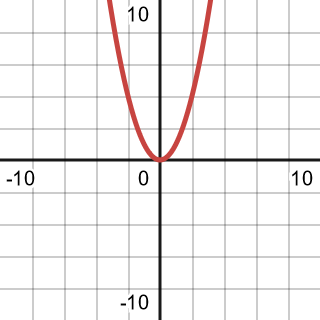$f(x) = x^2$
Cubic	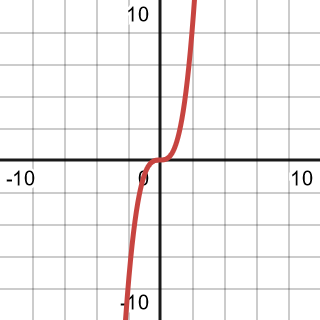$f(x) = x^3$
Reciprocal	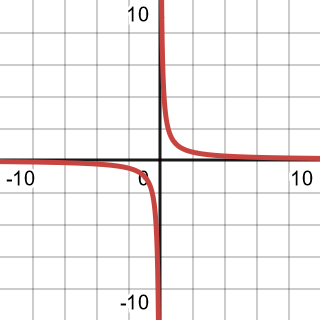$f(x) = \frac{1}{x}$
Reciprocal Squared	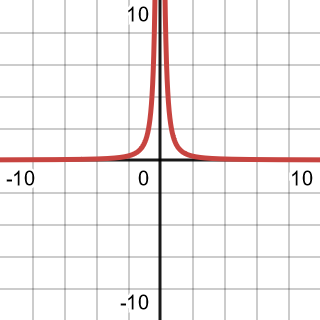$f(x) = \frac{1}{x^2}$
Square Root	$f(x) = \sqrt{x}$
Cube Root	$f(x) = \sqrt[3]{x}$