Function Behaviors

When we are analyzing functions, we need to have ways to describe the behaviors of said functions. Some common things we use to describe the behavior of functions include the average rate of change, whether it is increasing, decreasing, or constant, and the minimums and maximums found in the function.

Rate of Change

The rate of change describes how an output quantity changes relative to the change in the input quantity. Most time espically with real world data, the rate of change is not constant so we use the average rate of change over a specified period of time. The formula for average rate of change is...

$\text{Average rate of change}=\frac{\text{Change in output}}{\text{Change in input}} = \frac{\Delta{y}}{\Delta{x}} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{f(x_2) - f(x_1)}{x_2 - x_1}$

note

The symbol $\Delta$ means the change in a quantity. For example, $\Delta f$ means the change in $f$.

An example of average rate of change is...

$\underline{Example}$

Find the average rate of change of $f(x) = x - 2\sqrt{x}$ on the interval $[1, 9]$.

Let $x_1 = 1$ and $x_2 = 9$

$y_1 = 1 - 2\sqrt{1} = 1 - 2(1) = 1 - 2 = -1$

$y_2 = 9 - 2\sqrt{9} = 9 - 2(3) = 9 - 6 = 3$

$\frac{\Delta{y}}{\Delta{x}} = \frac{3 - (-1)}{9 - 1} = \frac{4}{8} = \frac{1}{2}$

The average rate of change is $\frac{1}{2}$.

note

We can use any point to find the slope of a linear line however when we are finding the average rate of change we need to use the points at the endpoints of the interval because we cannot assume that the rate of change is constant.

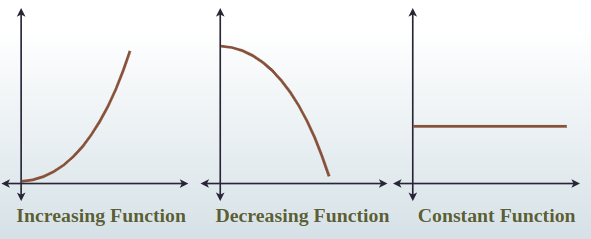
Increasing, Decreasing, or Constant

An useful method to describing the behavior of a function is to state if a function is increasing, decreasing, or constant over a given interval.

1. An increasing function is a function $f$ on an open interval if $f(b) > f(a)$ for any two input values $a$ and $b$ in a given interval where $b > a$.
2. A decreasing function is a function $f$ on an open interval if $f(b) < f(a)$ for any two input values $a$ and $b$ in the given interval where $b > a$.
3. A constant function is a function $f$ on an open interval if $f(b) = f(a)$ for any two input values $a$ and $b$.

Fig. 1 - Increasing, Decreasing, and Constant Functions

For the most common functions...

Name	Function	Increasing \ Decreasing
Constant	$f(x) = c$	Always constant
Identity	$f(x) = x$	Increasing
Quadratic	$f(x) = x^2$	Increasing on $(0, \infty)$ and Decreasing on $(-\infty, 0)$
Cubic	$f(x) = x^3$	Increasing
Reciprocal	$f(x) = \frac{1}{x}$	Decreasing $(-\infty, 0) \cup (0, \infty)$
Reciprocal Squared	$f(x) = \frac{1}{x^2}$	Increasing on $(-\infty, 0)$ and Decreasing on $(0, \infty)$
Cube Root	$f(x) = \sqrt[3]{x}$	Increasing
Square Root	$f(x) = \sqrt{x}$	Increasing on $(0, \infty)$
Absolute Value	$f(x) = \:\mid x \mid$	Increasing on $(0, \infty)$ and Decreasing on $(-\infty, 0)$

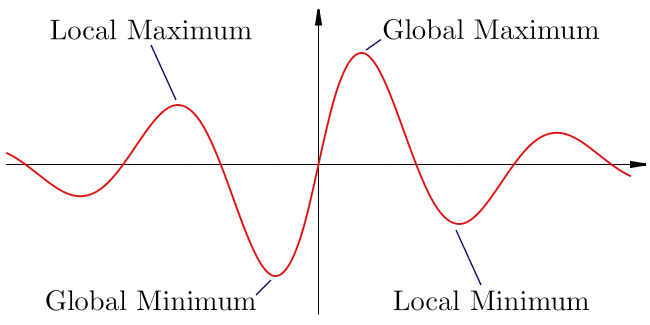
Minimum and Maximum

We use the minimum and maximums of a function to help describe all the peaks and valleys that a function may have and also help us understand where the function changes from increasing to decreasing or decreasing to increasing.

The output of the input where a function changes from decreasing to increasing is called the local minimum. In other words, the function $f$ has a local minimum at $x = b$ if there exists an interval $(a, c)$ with $a < b < c$ such that, for any $x$ in the interval $(a, c)$, $f(x) \geq f(b)$.

The output of the input where a function changes from increasing to decreasing is called the local maximum. In other words, the function $f$ has a local maximum at $x = b$ if there exists an interval $(a, c)$ with $a < b < c$ such that, for any $x$ in the interval $(a, c)$, $f(x) \leq f(b)$.

note

If a function has more than one local minimum, we say it has local minima. On the other hand, if the function has more than one local maximum, we use the plural form local maxima to express all of them. Together, the local maxima and minima are called the local extrema or local extreme values.

Also note that sometimes we can encounter the word local replaced with relative which means the same thing.

The absolute minimum of $f$ at $x = c$ is $f(c) \leq f(x)$ for all $x$ in the domain of $f$.

The absolute maximum of $f$ at $x = c$ is $f(c) \geq f(x)$ for all $x$ in the domain of $f$.

Fig. 2 - Minimums and Maximums