Function Transformation

In mathematics, we have systematic ways to alter the basic functions to build new functions out of them. This allows us to have better understanding of how to change functions and how operations on a function impact the look and behavior of the said function.

Vertical and Horizontal Shift

One basic transformation involves shifting the entire graph of a function up, down, left or right. Given a function $f(x)$...

1. The vertical shift shifts $f(x)$ up or down. Let $g(x) = f(x) + k$ where $k$ is a constant, this new function is a vertical shift of $f(x)$ by $k$ units. If $k$ is positive, the graph will shift up. If $k$ is negative, the graph will shift down.
2. The horizontal shift shifts $f(x)$ left or right. Let $g(x) = f(x - h)$ where $h$ is a constant, this new function is a horizontal shift of $f(x)$ by $h$ units. If $h$ is positive, the graph will shift right. If $h$ is negative, the graph will shift left.

Putting these concepts together, $g(x) = f(x - h) + k$ is a new function that shifts $f(x)$ vertically by $k$ units and horizontally by $h$ units. An example of this is...

$\underline{Example}$

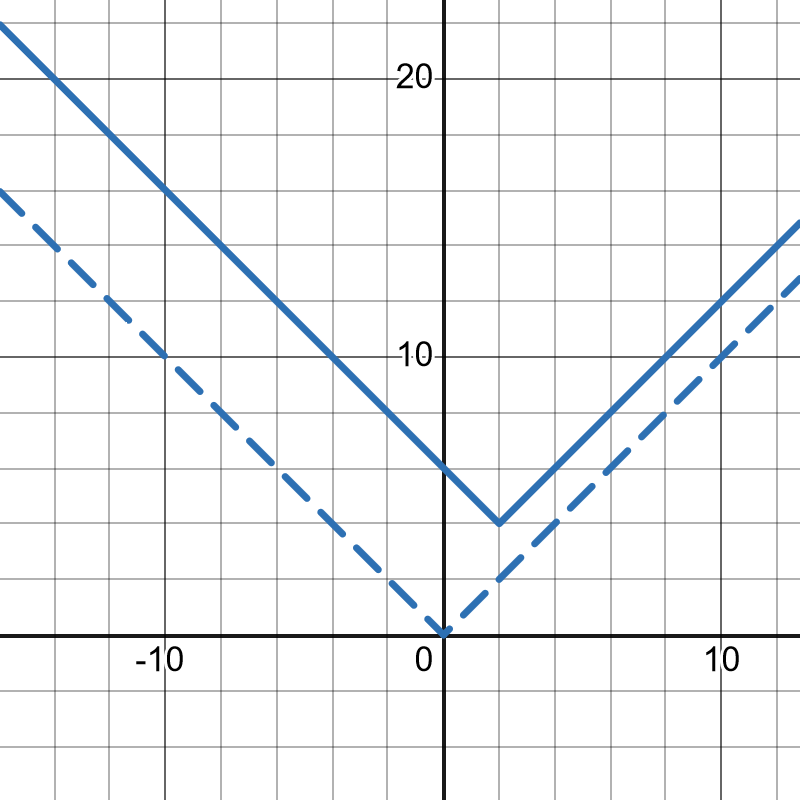
Given $f(x) = \:\mid x \mid$, describe the shifts to get $\:h(x) = \:\mid x - 2 \mid + \:4$.

In this instance, $k = 4$ and $h = 2$.

We shift $f(x)$ two units to the right and four units up to get $h(x)$.

Fig. 1 - Dashed Graph f(x) and Solid Graph = h(x)

Reflection

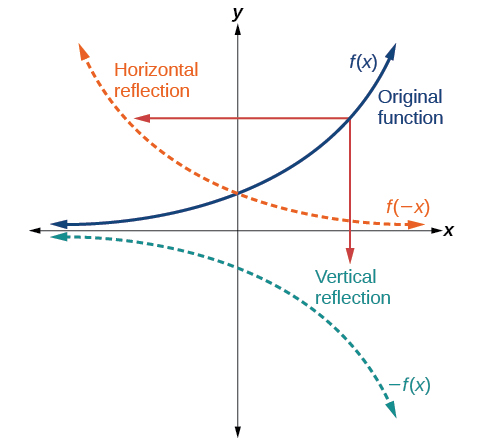
Another transformation that can be applied to a function is a reflection over the $x$ or $y$ axis. Given a function $f(x)$...

1. The vertical reflection reflects $f(x)$ over the $x$-axis. The function $g(x)$ is a reflection of $f(x)$ over the $x$-axis if $g(x) = -f(x)$.
2. The horizontal reflection reflects $f(x)$ over the $y$-axis. The function $g(x)$ is a reflection of $f(x)$ over the $y$-axis if $g(x) = f(-x)$.

For vertical reflection, we multiply all the outputs by $-1$ of the original function. Finally, for the horizontal reflection, we multiply all the inputs by $-1$ of the original function.

Fig. 2 - Reflection

Even and Odd Function

Some functions are symmetrical meaning when we reflect the function, we result in the original graph. There are two types of these functions...

1. An even function is a function whose graph is symmetric about the $y$-axis. This means for every $x$, $f(x) = f(-x)$. An example of an even function is $f(x) = x^2$ because $f(-x) = (-x)^2 = x^2$.
2. An odd function is a function whose graph is symmetric about the origin. This means for every $x$, $f(x) = -f(-x)$. An example of an odd function is $f(x) = x^3$ because $-f(-x) = -(-x)^3 = -1 \times -1 (x^3) = x^3$.

Strech and Compression

Finally, we can transform functions by stretching it or compressing it which changes the shape of the graph. Given a function $f(x)$...

1. Let $g(x) = af(x)$ where $a$ is a constant. A vertical stretch happens if $\mid a \mid\: > 1$. On the other hand, a vertical compression happens if $0 < \:\mid a \mid\: < 1$.
2. Let $g(x) = f(bx)$ where $b$ is a constant. A horizontal compression happens if $\mid b \mid\: > 1$ and in this case the graph will be compressed by $\frac{1}{b}$. On the other hand, a horizontal stretch happens if $0 < \:\mid a \mid\: < 1$ and in this case the graph will be stretched by $\frac{1}{b}$.

Fig. 3 - Stretch and Compression

note

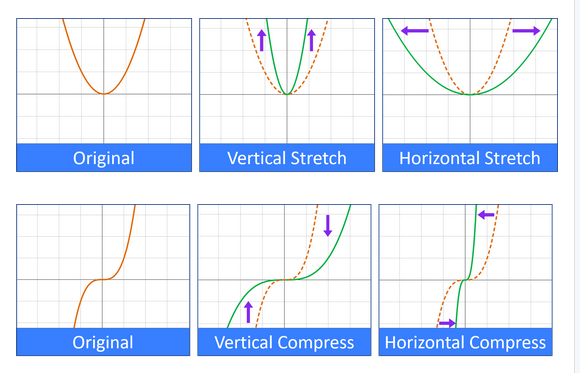
The sign of the constants $a$ and $b$ does not transform the stretch or compression but instead transforms the reflection of the graphs.

With all our transformations put together, we get the equation...

$g(x) = \pm a \times f(\pm b(x - h)) + k$

where $\pm a$ transforms by vertical stretch or compression and vertical reflection, $\pm b$ transforms by horizontal stretch or compression and horizontal reflection, $h$ transforms by horizontal shift, and $k$ transforms by vertical shift.