Inverse Functions

Some functions (one-to-one) have the ability to work backwards meaning we can reverse the nature of functions. An inverse function is a function for which the input of the original function becomes the output of the inverse function and the output of the original function becomes the input of the inverse function.

For any one-to-to function $f(x) = y$, we use the notation $f^{-1}(x)$ to signify the inverse function of $f(x)$. We read $f^{-1}$ as "$f$ inverse" and $f^{-1}(x)$ as "$f$ inverse of $x$".

Domain and Range

As previously stated, the range of the function $f(x)$ is the domain of the inverse function $f^{-1}(x)$. Vice versa, the domain of $f(x)$ is the range of $f^{-1}(x)$.

If the original function is one-to-one, we can inverse the domain and range. If the original function is not one-to-one, we need to restrict the domain of $f(x)$ in order to make it one-to-one and then we can use this as the range of the inverse function.

Evaluation

Given the graph or table of a function, we can evaluate the inverse at specific points by finding the input on the y-axis or output column. We read the x-axis or input column to get our point.

If we have the original formula, we can find the inverse function. We first need to verify $f$ is an one-to-one function and then solve for $x$. After that we interchange $x$ and $y$ and then replace $y$ with $f^{-1}(x)$. The variables can be different in many cases but the principal is the same.

$\underline{Example}$

Given the function $C = \frac{5}{9}(F - 32)$, find the inverse function.

The domain and range are both $(-\infty, \infty)$ for both functions.

We can interchange the input and output values into $F = \frac{5}{9}(C - 32)$.

$\frac{9}{5}F = C - 32$

$C = \frac{9}{5}F + 32$

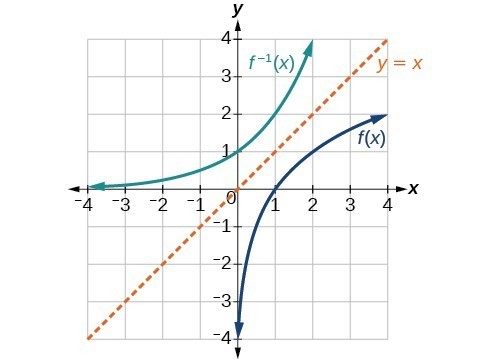
Graphs

If we graph any $f(x)$ and $f^{-1}(x)$ then we can see a pattern. All graphs of $f^{-1}(x)$ is the graph of $f(x)$ reflected about the diagonal line $y = x$, which we call the identity line.

Fig. 1 - Relationship between inverses