Exponential Functions

So far we have worked with linear growth which refers to when the original value from the range increases by the same amount over equal increments found in the domain. In contrast, exponential growth refers to when the original value from the range increases by the same percentage over equal increments found in the domain. Due to percent change, exponential growth will grow rapidly as the $x$ increases.

Some common terms encountered when dealing with exponential functions include...

1. Percent change: a change based on a percent of the original amount.
2. Exponential growth: an increase based on a constant multiplicative rate of change over equal increments of time, that is, a percent increase of the original amount over time.
3. Exponential decay: a decrease based on a constant multiplicative rate of change over equal increments of time, that is, a percent decrease of the original amount over time.

Exponential Functions

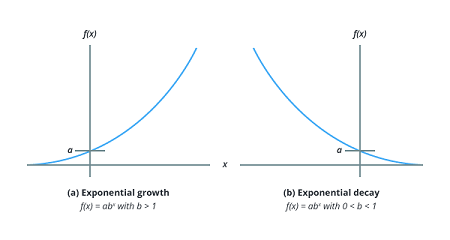
In general, for any real number $x$, an exponential function is a function with the form $f(x) = ab^x$ where $a$ is a non-zero real number indicating the initial value and $b$ is any positive real number indicating the base such that $b \neq 1$.

Exponential functions have quite a few properties that we can extract using the form...

1. The domain of $f$ is all real numbers.
2. The range of $f$ is all positive real numbers if $a > 0$ and the range of $f$ is all negative real numbers if $a < 0$.
3. The $y$-intercept is $(0, a)$.
4. The horizontal asymptote is $y = 0$.
5. The function models exponential growth if $b > 1$ and the function models exponential decay if $0 < b < 1$.

Fig. 1 - Exponential Growth and Decay

note

The base $b$ is restricted to positive values to ensure that the outputs will be real numbers. For example, if we let $a = 1$, $b = -9$ and $x = \frac{1}{2}$. Then $f(x) = f(\frac{1}{2}) = 1(-9)^{\frac{1}{2}} = \sqrt{-9}$, which is not a real number.

Just like with other functions, we can evaluate an exponential function for any $x$-value by substituting the value in the function and simplifying...

$\underline{Example}$

Let $f(x) = 5(3)^{x + 1}$. Evaluate $f(2)$ without using a calculator.

$$\begin{array}{l} f(x) = 5(3)^{x + 1} \\ f(2) = 5(3)^{2 + 1} \:\:\: \text{Substitute for } x. \\ \phantom{f(2)} = 5(3)^3 \:\:\: \text{Add the exponents.} \\ \phantom{f(2)} = 5(27) \:\:\: \text{Simplify the power.} \\ \phantom{f(2)} = 135 \:\:\: \text{Multiply.} \end{array}$$

Finding Equations

Given two data points, we can write an exponential model in the form of $f(x) = a(b)^x$. If one of the data points has the form $(0, a)$, then $a$ is the initial value. Using $a$, we can substitute the second point into the equation $f(x) = a(b)^x$ to solve for $b$. On the other hand, if neither of the data points have the form $(0, a)$, we can substitute both points into two equations with the form $f(x) = a(b)^x$. After this, we can solve the resulting system of two equations in two unknowns to find $a$ and $b$. In both of these case, we want to use the value of $a$ and $b$ to write the function in the form $f(x) = a(b)^x$.

Let's look at the case where we have a point in the form $(0, a)$...

$\underline{Example}$

A wolf population is growing exponentially. In $2011$, $129$ wolves were counted. By $2013$, the population had reached $236$ wolves. What two points can be used to derive an exponential equation modeling this situation? Write the equation representing the population $N$ of wolves over time $t$.

The initial population was counted in $2011$ so our first data point is $(0, 129)$ and $t$ is the number of years after $2011$. This means our second data point is $(2, 236)$ which is the count of wolves in $2013$.

Due to the fact that $(0, 129)$ is in the form $(0, a)$, we can conclude that $a = 129$.

We can substuting $a = 129$ and $(2, 236)$ in $N(t) = a(b)^t$ to find the value of $b$...

$N(t) = a(b)^t \to 236 = 129(b)^2 \to 1.8295 \approx b^2 \to 1.3526 \approx b$

The wolf population can be modelled using $N(t) = 129(1.3526)^t$ where $t$ is the number of years after $2011$.

Now let's look at the case where neither of the points are in the form $(0, a)$...

$\underline{Example}$

Given the two points $(1, 3)$ and $(2, 4.5)$, find the equation of the exponential function that passes through these two points.

Because neither of the data points represent the initial value, we need to substitute each point into an equation of the form $f(x) = ab^x$, and then solve the system of equations for $a$ and $b$.

If we substitute $(1, 3)$, we get $3 = ab^1$.

If we substitute $(2, 4.5)$, we get $4.5 = ab^2$.

We can solve either equation for $a$ in terms of $b$. If we solve for $3 = ab^1$, we get $3 = ab \to a = \frac{3}{b}$.

We can substitute $a = \frac{3}{b}$ into the second equation and solve for $b$...

$4.5 = ab^2 \to 4.5 = (\frac{3}{b})b^2 \to 4.5 = \frac{3b^2}{b} \to 4.5 = 3b \to \frac{4.5}{3} = b \to 1.5 = b$

We can now substitute the value of $b$ into either equation to get the value of $a$...

$3 = ab \to 3 = a(1.5) \to \frac{3}{1.5} = a \to 2 = a$

By substituting for $a$ and $b$, the equation is $f(x) = 2(1.5)^x$.

Compound Interest

Compound interest refers to interest earned not only on the original value, but on the accumulated value of the account. This concept of compounding is often found with savings instruments in which earnings are continually reinvested like mutual funds and retirement accounts. The annual percentage rate (APR) of these accounts is the yearly interest rate earned by these account. We also refer to them this as the nominal rate because the term nominal is used when the compounding occurs more than once in year causing the effective interest rate to be greater than the nominal rate.

Compound interest can be calculated using the formula $A(t) = P(1 + \frac{r}{n})^{nt}$ where $A(t)$ is the account value, $P$ is the principal/starting amount, $r$ is the APR expressed as a decimal, $n$ is the number of compounding periods in one year, and $t$ is the number of years.

$\underline{Example}$

An initial investment of $\$100{,}000$ at $12\%$ interest is compounded weekly (use $52$ weeks in a year). What will be the investment be worth in $30$ years?

From the problem, we can obtain the following information...

1. The initial investment is $\$100{,}000$ so $P = 100{,}000$.
2. The interest rate is $12\%$ which represents the APR so $r = 0.12$.
3. The interest is compounded weekly so $n = 52$.
4. We are looking for the $A(t)$ in $30$ years so $t = 30$ and we are solving for $A(t)$.

We can substitute all the given values into the compound interest formula and them solving for $A(t)$...

$$\begin{array}{l} A(t) = P(1 + \frac{r}{n})^{nt} \\ \phantom{A(t)} = 100000(1 + \frac{0.12}{52})^{52(30)} \\ \phantom{A(t)} \approx 100000(1.00231)^{1560} \\ \phantom{A(t)} \approx 100000(36.44676) \\ \phantom{A(t)} \approx 3644675.88 \end{array}$$

The investment after $30$ years is worth $\$3{,}644{,}675.88$.

Euler's Number

The amount earned on an account increases as the compound frequency increases. This means as we increase the value of $n$ and keep everything else the same in the compound interest formula, the value of $A(t)$ should always increase.

Euler's number is a number which is represented by the letter $e$ and this represents the irrational number found by increasing $n$ without bound for $(1 + \frac{1}{n})^n$. This number approximates to $e \approx 2.718282$ and is irrational because as previously stated, $A(t)$ will never stop increasing as $n$ increases. The value of $e$ is the value that the function $(1 + \frac{1}{n})^n$ converges to as it approaches infinity.

The constant was named by the Swiss mathematican Leonhard Euler who first investigated and discovered many of its properties and this number is used as a base for countless real-world exponential models.

Continuous Growth and Decay

For most real-world phenomena, $e$ is used as the base for exponential functions and these models that use $e$ as the base are called continuous growth or decay models. For all real numbers $t$, and all positive numbers $a$ and $r$, continuous growth or decay is represented by the formula $A(t) = ae^{rt}$ where $a$ is the initial value, $r$ is the continuous growth rate per unit time, and $t$ is the elapsed time. Note that if $r > 0$, then the formula represents continuous growth and if $r < 0$, then the formula represents continuous decay.

$\underline{Example}$

Radon-222 decays at a continuous rate of $17.3\%$ per day. How much will $100$ mg of Radon-222 decay to after one year?

Based on the problem, our known quantities are...

1. We are decaying at a rate of $17.3\%$. This means $r = -0.173$. Note that if we were growing instead of decaying then $r$ would be positive.
2. Our initial value is $100$ mg so $a = 100$.
3. We are looking for the amount remaining after $1$ year so $t = 365$. We had to convert year into days as the decay occurs every day.

Using $a = 100$, $r = -0.173$, and $t = 365$, we can solve for $A(t)$...

$$\begin{array}{l} A(t) = ae^{rt} \\ \phantom{A(t)} = 100e^{-0.173(365)} \\ \phantom{A(t)} = 100e^{-63.145} \\ \phantom{A(t)} \approx 100(3.77 \times 10^{-28}) \\ \phantom{A(t)} \approx 3.77 \times 10^{-26} \end{array}$$

There will be about $3.77 \times 10^{-26}$ mg of Radon-222 left after $1$ year.

When working with business applications, the continuous growth formula is called the continuous compounding formula and takes the form $A(t) = Pe^{rt}$ where $P$ is the principal or the initial invested, $r$ is the growth or interest rate per unit time, and $t$ is the period or term of the investment.

$\underline{Example}$

A person invests $\$100{,}000$ at a nominal $12\%$ interest per year compounded continuously. What will be the value of the investment in $30$ years?

Based on the problem, our known quantities are...

1. Our initial investment is $\$100{,}000$ so $P = 100000$.
2. There is an interest of $12\%$ applied per year so $r = 0.12$.
3. We want to find $A(t)$ after $30$ years and the interest is applied per year so $t = 30$.

Using $P = 100000$, $r = 0.12$, and $t = 30$, we can solve for $A(t)$...

$$\begin{array}{l} A(t) = Pe^{rt} \\ \phantom{A(t)} = 100000e^{0.12(30)} \\ \phantom{A(t)} = 100000e^{3.6} \\ \phantom{A(t)} \approx 100000(36.5982344) \\ \phantom{A(t)} \approx 3659823.44 \end{array}$$

After $30$ years, the investment will be worth about $\$3{,}659{,}823.44$.