Logarithmic Functions

Many functions and operations in mathematics have ways to inverse themselves. For example, subtraction is an inverse of addition, division is an inverse of multiplication, and square root functions are an inverse of quadratic functions. Exponential functions can also be inverted and that is through logarithmic functions.

Logarithms

A logarithm of base $b$ where $b > 0$ and $b \neq 1$ of $x$ where $x > 0$ is denoted as $\log_b(x)$ which is equivalent to $b^y = x$. When we read $\log_b(x)$, we stated "the logarithm base $b$ of $x$" or "log base $b$ of $x$".

Since, $b^y = x$ and $\log_b(x) = y$ are inverses, we can infer that the logarithm $y$ is the exponent to which $b$ must be raised to get $x$. Also due to the fact that we switch the $x$ and $y$ values, the domain and range of the exponential function are switched for the logarithmic function. This means the domain of the logarithmic function is $(0, \infty)$ and the range is $(-\infty, \infty)$.

Fig. 1 - Exponential and Logarithmic Graph

note

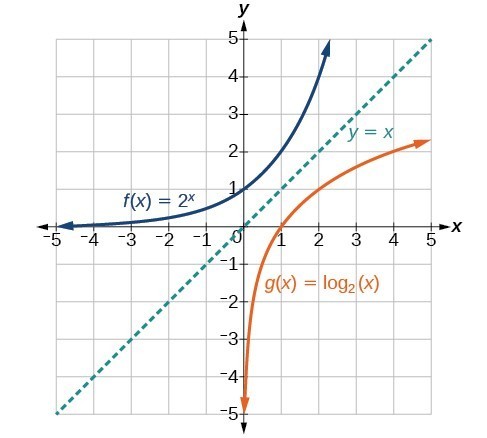
Exponential functions are one-to-one functions which allows us to have inverse functions. This also means that logarithmic functions are one-to-one functions.

Converting Forms

Given an equation in logarithmic form $\log_b(x) = y$, we can convert it to exponential form by first examining the equation and identifying the values of $b$, $y$, and $x$. We can then substitute these values into $b^y = x$ to get our converted form.

$\underline{Example}$

Write the equation $\log_5 (25) = 2$ in exponential form.

Using the equation, we can identify that $b = 5$, $x = 25$, and $y = 2$.

Substituting these values into $b^y = x$ gives a solution of $5^2 = 25$.

The process of converting forms from exponential functions to logarithmic functions is similar to our process above. Given an equation in exponential form $b^y = x$, we can convert it to logarithmic form by first examining the equation and identifying the values of $b$, $y$, and $x$. We can then substitute these values into $\log_b(x) = y$ to get our converted form.

$\underline{Example}$

Write the equation $2^3 = 8$ in exponential form.

Using the equation, we can identify that $b = 2$, $y = 3$, and $x = 8$.

Substituting these values into $\log_b(x) = y$ gives a solution of $\log_2(8) = 3$.

Evaluation

Given a logarithm of the form $y = \log_b(x)$, we can evaluate it mentally. Firstly, we rewrite the argument $x$ as a power of $b$ which gives us $b^y = x$. After this we use previous knowledge of powers of $b$ to identify $y$ by asking: "What exponent should $b$ be raised in order to get $x$?".

$\underline{Example}$

Evaluate $y = \log_2(\frac{1}{32})$.

Firstly, rewriting this in exponential form, we get $2^y = \frac{1}{32}$. Next, we ask, "To what exponent must $2$ be raised in order to get $\frac{1}{32}$?".

We know that $2^5 = 32$, but we need to reciprocal of this. We can use the property of exponents where $b^{-a} = \frac{1}{b^a}$ to get $2^{-5} = \frac{1}{2^5} = \frac{1}{32}$.

Therefore, $\log_2(\frac{1}{32}) = -5$.

Common Logarithms

A common logarithm is a logarithm with base $10$ which we can also write as $\log(x)$ instead of $\log_{10}(x)$. Whenever the base is omitted from the logarithmic function, we are refering to the common logarithm. The common logarithm still follows the same rules as other logarithms meaning for $x > 0$, $y = \log(x)$ is equivalent to $10^y = x$ and the logarithm $y$ is the exponent to which $10$ must be raised to get $x$. Finally, we read $\log(x)$ as, "the logarithm with base $10$ of $x$" or "log base $10$ of $x$".

Natural Logarithms

A natural logarithm is a logarithm with base $e$ which we can also write as $\ln(x)$ instead of $\log_e(x)$. The natural logarithm still follows the same rules as other logarithms meaning for $x > 0$, $y = \ln(x)$ is equivalent to $e^y = x$ and the logarithm $y$ is the exponent to which $e$ must be raised to get $x$. Finally, we read $\ln(x)$ as, "the logarithm with base $e$ of $x$" or "the natural logarithm of $x$".

note

Since the functions $y = e^x$ and $y = \ln(x)$ are inverse functions, $\ln(e^x) = x$ for all $x$ and $e^{\ln(x)} = x$ for $x > 0$.