Inequalities

Equations allow us to compare two values or expressions exactly. But, there are countless times in mathematics where we want to express a relationship between two expressions where they are not equal. This is exactly the role that inequalities serve. Inequalities are used to compare two values or expressions that are not equal.

The symbols we use to describe inequalities are...

Symbol	Definition
$>$	Greater than
$<$	Less than
$\geq$	Greater than or equal to
$\leq$	Less than or equal to

Properties of Inequalities

There are two properties of inequalities, the addition property and the multiplication property.

The addition property states if $a < b$, then $a + c < b + c$.

The multiplication property states if $a < b$ and $c > 0$, then $ac < bc$. On the other hand, if $a < b$ and $c < 0$, then $ac > bc$. This means we keep the symbol the same if $c > 0$ and reverse the symbol if $c < 0$.

note

These properties also apply to $a \leq b$, $a > b$, and $a \geq b$.

Solving Inequalities

When working with inequalities, we can treat then similarly to equations by using the same algebraic rules. It is similar but not exact because when we are multiplying or dividing by a negative number in an inequality, we reverse the inequality symbol. Besides that fact, in order to solve an inequality, our goal is to still isolate the variable to one side.

$\underline{Example}$

$-x + 4 < \frac{1}{2}x + 2$

$-2x + 8 < x + 2$

$-3x < -6$

$x > \frac{-6}{-3}$

$x > 2$

Compound Inequalities

A compound inequality is an inequality which includes two inequalities in one statement like $-5 < x \leq 12$.

There are two ways to solve such inequalities. One method is to seperate the compound inequality into two seperate inequalities and solve them individually. The alternative method is to apply the same operations to all three parts at the same time.

$\underline{Example}$

$4 < 2x - 8 \leq 10$

$4 + 8 < 2x - 8 + 8 \leq 10 + 8$

$12 < 2x \leq 18$

$\frac{12}{2} < \frac{2x}{2} \leq \frac{18}{2}$

$6 < x \leq 9$

note

If we wanted to solve the above example through the first method, we would solve for $4 < 2x - 8$ and $2x - 8 \leq 10$ seperately. At the end we would combine the two solutions and would still arrive at $6 < x \leq 9$.

Absolute Value Inequalities

An absolute value inequality is an inequality which includes an absolute value. Given an algebraic expression $X$, and $k > 0$...

Absolute Value Inequality	Equivalent Inequality
$\mid X \mid \: < k$	$-k < X < k$
$\mid X \mid \: \leq k$	$-k \leq X \leq k$
$\mid X \mid \: > k$	$X < -k$ or $X > k$
$\mid X \mid \: \geq k$	$X \leq -k$ or $X \geq k$

Putting this into practice...

$\underline{Example}$

$-2|x - 4| \leq -6$

$|x - 4| \geq 3$

$x - 4 \leq -3$ or $x - 4 \geq 3$

$x \leq 1$ or $x \geq 7$

Expressing Solutions to Inequalities

There are three ways to express the solution to an inequality. The first method is through a number line. We draw points at the endpoints of the solution set where the point is shaded if it is included in the set and open if it is not included in the set. Finally, we draw a line through all the numbers in the set and an arrowhead if it continues towards infinity.

Fig. 1 - Plotting x < 1

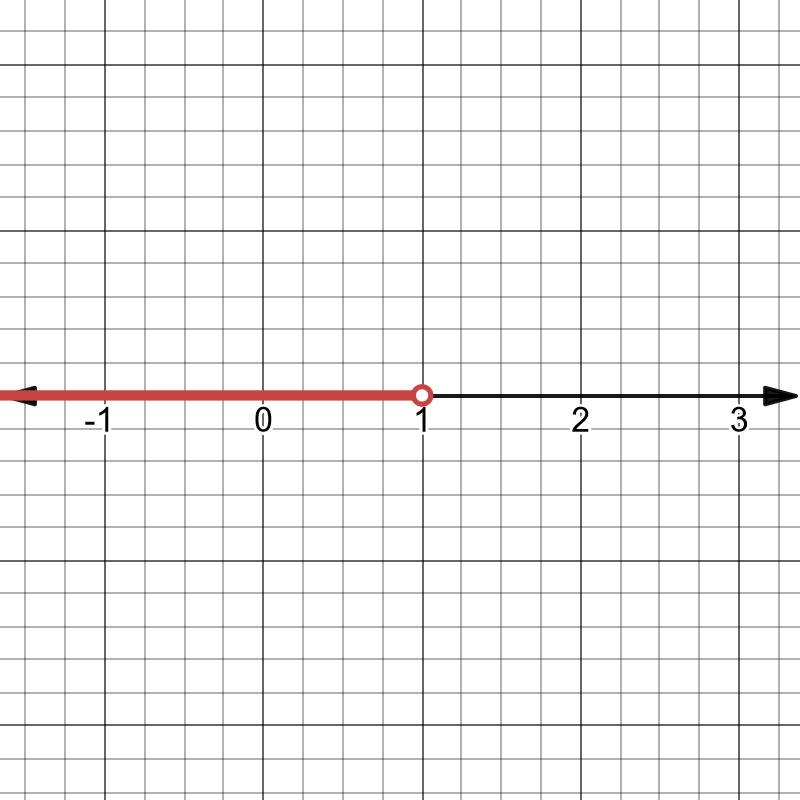
The second way is to use set-builder notation where we write $\{x\:|$ (conditions or properties of $x$)$\}$. For example, $x < 1$ can be expressed as $\{x|x < 1\}$.

The final way is to use interval notation where we state the range of numbers included in the set. We use brackets to state that the number is included in the solution set and parenthesis to state that the number is not included in the solution set. If the solution tends towards infinity, we use the infinity symbol and also use paranthesis as we cannot include infinity in our solution set. For example, we can express $x < 1$ as $(-\infty, 1)$.

Possibilities for set-builder notation and interval notation include...

Verbal	Set-Builder Notation	Interval Notation
All real numbers between $a$ and $b$, but not including $a$ or $b$	$\{x \mid a < x < b\}$	$(a, b)$
All real numbers greater than $a$, but not including $a$	$\{x \mid x > a\}$	$(a, \infty)$
All real numbers less than $b$, but not including $b$	$\{x \mid x < b\}$	$(-\infty, b)$
All real numbers greater than $a$, including $a$	$\{x \mid x \geq a\}$	$[a, \infty)$
All real numbers less than $b$, including $b$	$\{x \mid x \leq b\}$	$(-\infty, b]$
All real numbers between $a$ and $b$, including $a$	$\{x \mid a \leq x < b\}$	$[a, b)$
All real numbers between $a$ and $b$, including $b$	$\{x \mid a < x \leq b\}$	$(a, b]$
All real numbers between $a$ and $b$, including $a$ and $b$	$\{x \mid a \leq x \leq b\}$	$[a, b]$
All real numbers less than $a$ or greater than $b$	$\{x \mid a < x \:or\: x > b\}$	$(-\infty, a) \cup (b, \infty)$
All real numbers	$\{x \mid x\:is\:all\:real\:numbers\}$	$(-\infty, \infty)$