Sum and Difference Identities Finding the exact value of the sine, cosine, or tangent of an angle is often easier if we can rewrite a given angle as a sum or difference of two angles that we know the exact value for. For example, we can't currently find the exact value of sin ( 1 5 ∘ ) \sin(15^\circ) sin ( 1 5 ∘ ) sin ( 4 5 ∘ − 3 0 ∘ ) \sin(45^\circ - 30^\circ) sin ( 4 5 ∘ − 3 0 ∘ )
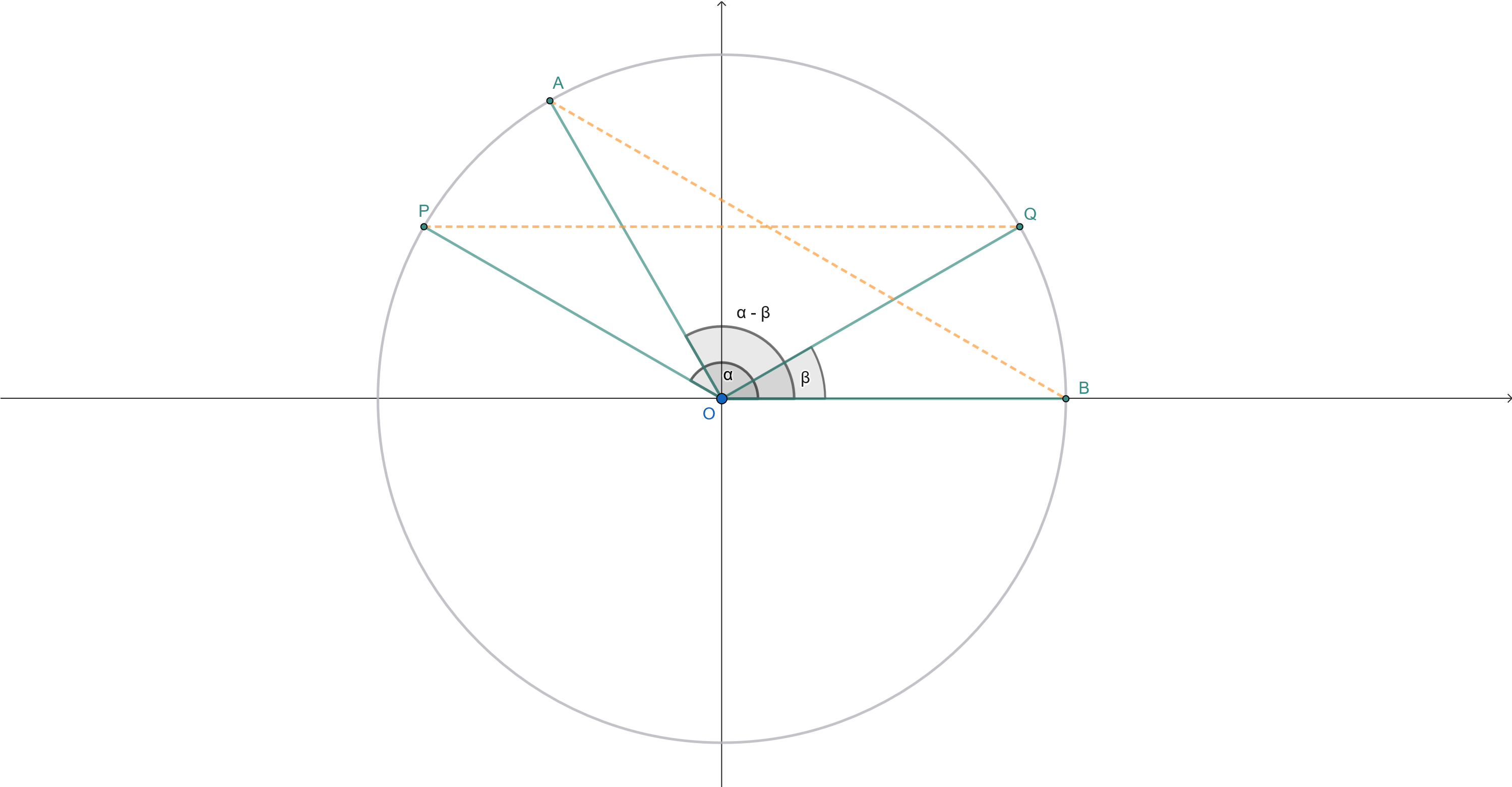
Difference of Cosine To derive all the sum and difference identities, we will begin by deriving the difference formula for cosine. Let's begin by drawing an angle α \alpha α x x x ( cos α , sin α ) (\cos \alpha, \sin \alpha) ( cos α , sin α ) P P P β \beta β Q Q Q ( cos β , sin β ) (\cos \beta, \sin \beta) ( cos β , sin β ) ∠ P O Q \angle POQ ∠ POQ O O O α − β \alpha - \beta α − β
Before we can derive the formula, we also need to plot two additional points. The first point is A A A α − β \alpha - \beta α − β ( cos ( α − β ) , sin ( α − β ) ) (\cos(\alpha - \beta), \sin(\alpha - \beta)) ( cos ( α − β ) , sin ( α − β )) B B B x x x ( 1 , 0 ) (1, 0) ( 1 , 0 )
Fig. 1 - Difference of Cosine The angles ∠ A O B \angle AOB ∠ A OB ∠ P O Q \angle POQ ∠ POQ α − β \alpha - \beta α − β △ A O B \triangle AOB △ A OB △ P O Q \triangle POQ △ POQ A B AB A B P Q PQ PQ cos ( α − β ) \cos(\alpha - \beta) cos ( α − β ) cos α \cos \alpha cos α cos β \cos \beta cos β
The length of segment P Q PQ PQ P = ( cos α , sin α ) P = (\cos \alpha, \sin \alpha) P = ( cos α , sin α ) Q = ( cos β , sin β ) Q = (\cos \beta, \sin \beta) Q = ( cos β , sin β )
PQ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 = ( cos β − cos α ) 2 + ( sin β − sin α ) 2 = ( cos 2 β − 2 cos α cos β + cos 2 α ) + ( sin 2 β − 2 sin α sin β + sin 2 α ) = ( cos 2 α + sin 2 α ) + ( cos 2 β + sin 2 β ) − 2 cos α cos β − 2 sin α sin β = 1 + 1 − 2 ( cos α cos β + sin α sin β ) = 2 − 2 ( cos α cos β + sin α sin β ) \begin{array}{lllllllll} \text{PQ} &=& \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \\[1em] &=& \sqrt{(\cos \beta - \cos \alpha)^2 + (\sin \beta - \sin \alpha)^2} \\[1em] &=& \sqrt{(\cos^2 \beta - 2\cos \alpha \cos \beta + \cos^2 \alpha) + (\sin^2 \beta - 2\sin \alpha \sin \beta + \sin^2 \alpha)} \\[1em] &=& \sqrt{(\cos^2 \alpha + \sin^2 \alpha) + (\cos^2 \beta + \sin^2 \beta) - 2\cos \alpha \cos \beta - 2\sin \alpha \sin \beta} \\[1em] &=& \sqrt{1 + 1 - 2(\cos \alpha \cos \beta + \sin \alpha \sin \beta)} \\[1em] &=& \sqrt{2 - 2(\cos \alpha \cos \beta + \sin \alpha \sin \beta)} \\[1em] \end{array} PQ = = = = = = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ( cos β − cos α ) 2 + ( sin β − sin α ) 2 ( cos 2 β − 2 cos α cos β + cos 2 α ) + ( sin 2 β − 2 sin α sin β + sin 2 α ) ( cos 2 α + sin 2 α ) + ( cos 2 β + sin 2 β ) − 2 cos α cos β − 2 sin α sin β 1 + 1 − 2 ( cos α cos β + sin α sin β ) 2 − 2 ( cos α cos β + sin α sin β ) Next, the length of segment A B AB A B A = ( cos ( α − β ) , sin ( α − β ) ) A = (\cos(\alpha - \beta), \sin(\alpha - \beta)) A = ( cos ( α − β ) , sin ( α − β )) B = ( 1 , 0 ) B = (1, 0) B = ( 1 , 0 )
AB = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 = ( 1 − cos ( α − β ) ) 2 + ( 0 − sin ( α − β ) ) 2 = ( 1 − cos ( α − β ) ) 2 + ( − sin ( α − β ) ) 2 = ( 1 − 2 cos ( α − β ) + cos 2 ( α − β ) ) + ( sin 2 ( α − β ) ) = 1 − 2 cos ( α − β ) + ( cos 2 ( α − β ) + sin 2 ( α − β ) ) = 1 − 2 cos ( α − β ) + 1 = 2 − 2 cos ( α − β ) \begin{array}{lllllllll} \text{AB} &=& \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \\[1em] &=& \sqrt{(1 - \cos(\alpha - \beta))^2 + (0 - \sin(\alpha - \beta))^2} \\[1em] &=& \sqrt{(1 - \cos(\alpha - \beta))^2 + (-\sin(\alpha - \beta))^2} \\[1em] &=& \sqrt{(1 - 2\cos(\alpha - \beta) + \cos^2(\alpha - \beta)) + (\sin^2(\alpha - \beta))} \\[1em] &=& \sqrt{1 - 2\cos(\alpha - \beta) + (\cos^2(\alpha - \beta) + \sin^2(\alpha - \beta))} \\[1em] &=& \sqrt{1 - 2\cos(\alpha - \beta) + 1} \\[1em] &=& \sqrt{2 - 2\cos(\alpha - \beta)} \\[1em] \end{array} AB = = = = = = = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ( 1 − cos ( α − β ) ) 2 + ( 0 − sin ( α − β ) ) 2 ( 1 − cos ( α − β ) ) 2 + ( − sin ( α − β ) ) 2 ( 1 − 2 cos ( α − β ) + cos 2 ( α − β )) + ( sin 2 ( α − β )) 1 − 2 cos ( α − β ) + ( cos 2 ( α − β ) + sin 2 ( α − β )) 1 − 2 cos ( α − β ) + 1 2 − 2 cos ( α − β ) Finally, we can set the lengths of segments P Q PQ PQ A B AB A B cos ( α − β ) \cos(\alpha - \beta) cos ( α − β )
PQ = AB 2 − 2 ( cos α cos β + sin α sin β ) = 2 − 2 cos ( α − β ) 2 − 2 ( cos α cos β + sin α sin β ) = 2 − 2 cos ( α − β ) − 2 ( cos α cos β + sin α sin β ) = − 2 cos ( α − β ) cos α cos β + sin α sin β = cos ( α − β ) \begin{array}{cccccccc} \text{PQ} &=& \text{AB} \\[1em] \sqrt{2 - 2(\cos \alpha \cos \beta + \sin \alpha \sin \beta)} &=& \sqrt{2 - 2\cos(\alpha - \beta)} \\[1em] 2 - 2(\cos \alpha \cos \beta + \sin \alpha \sin \beta) &=& 2 - 2\cos(\alpha - \beta) \\[1em] -2(\cos \alpha \cos \beta + \sin \alpha \sin \beta) &=& -2\cos(\alpha - \beta) \\[1em] \cos \alpha \cos \beta + \sin \alpha \sin \beta &=& \cos(\alpha - \beta) \\[1em] \end{array} PQ 2 − 2 ( cos α cos β + sin α sin β ) 2 − 2 ( cos α cos β + sin α sin β ) − 2 ( cos α cos β + sin α sin β ) cos α cos β + sin α sin β = = = = = AB 2 − 2 cos ( α − β ) 2 − 2 cos ( α − β ) − 2 cos ( α − β ) cos ( α − β ) So, the derived formula for the difference of cosine is cos ( α − β ) = cos α cos β + sin α sin β \cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta cos ( α − β ) = cos α cos β + sin α sin β
Sum of Cosine We can derive the sum formula for cosine by using the difference of cosine because cos ( α + β ) = cos ( α − ( − β ) ) \cos(\alpha + \beta) = \cos(\alpha - (-\beta)) cos ( α + β ) = cos ( α − ( − β ))
cos ( α + β ) = cos ( α − ( − β ) ) = cos α cos ( − β ) + sin α sin ( − β ) = cos α cos β + sin α ( − sin β ) = cos α cos β − sin α sin β \begin{array}{cccccccc} \cos(\alpha + \beta) &=& \cos(\alpha - (-\beta)) \\[1em] &=& \cos \alpha \cos(-\beta) + \sin \alpha \sin(-\beta) \\[1em] &=& \cos \alpha \cos \beta + \sin \alpha (-\sin \beta) \\[1em] &=& \cos \alpha \cos \beta - \sin \alpha \sin \beta \\[1em] \end{array} cos ( α + β ) = = = = cos ( α − ( − β )) cos α cos ( − β ) + sin α sin ( − β ) cos α cos β + sin α ( − sin β ) cos α cos β − sin α sin β So, the derived formula for the sum of cosine is cos ( α + β ) = cos α cos β − sin α sin β \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta cos ( α + β ) = cos α cos β − sin α sin β
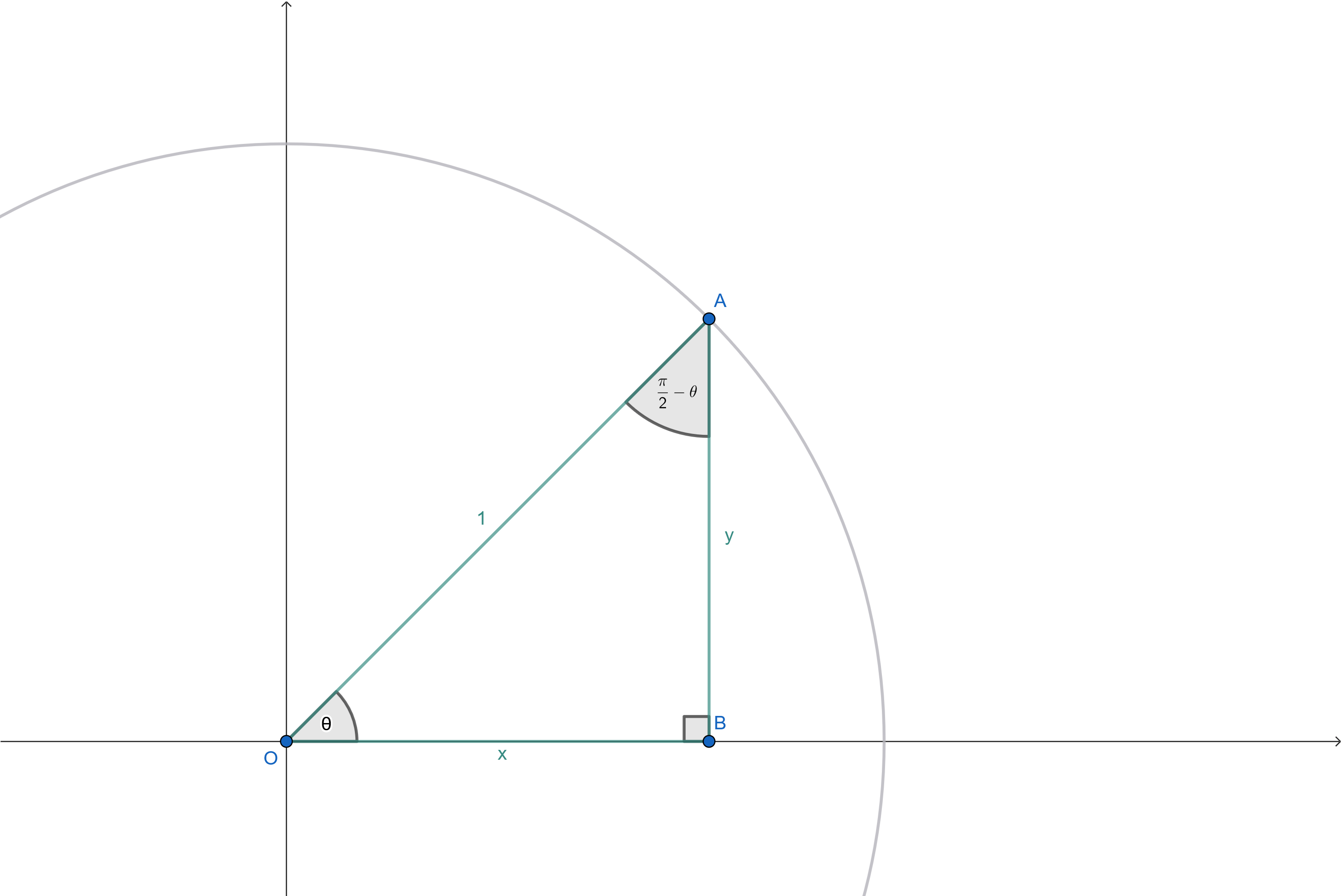
Cofunction Identities In order to derive the sum of sine formula, we need the cofunction identities. Let's begin by drawing a right triangle with an angle θ \theta θ ( x , y ) (x, y) ( x , y ) y y y x x x 1 1 1 1 1 1 θ \theta θ π 2 \frac{\pi}{2} 2 π π 2 − θ \frac{\pi}{2} - \theta 2 π − θ π \pi π
Fig. 2 - Cofunction Using the diagram, we can solve for the values of the six trigonometric functions for the angle θ \theta θ π 2 − θ \frac{\pi}{2} - \theta 2 π − θ
sin θ = y sin ( 9 0 ∘ − θ ) = x cos θ = x cos ( 9 0 ∘ − θ ) = y tan θ = y x tan ( 9 0 ∘ − θ ) = x y csc θ = 1 y csc ( 9 0 ∘ − θ ) = 1 x sec θ = 1 x sec ( 9 0 ∘ − θ ) = 1 y cot θ = x y cot ( 9 0 ∘ − θ ) = y x \begin{array}{lllllllll} \sin \theta = y && \sin(90^\circ - \theta) = x \\[1em] \cos \theta = x && \cos(90^\circ - \theta) = y \\[1em] \tan \theta = \frac{y}{x} && \tan(90^\circ - \theta) = \frac{x}{y} \\[1em] \csc \theta = \frac{1}{y} && \csc(90^\circ - \theta) = \frac{1}{x} \\[1em] \sec \theta = \frac{1}{x} && \sec(90^\circ - \theta) = \frac{1}{y} \\[1em] \cot \theta = \frac{x}{y} && \cot(90^\circ - \theta) = \frac{y}{x} \\[1em] \end{array} sin θ = y cos θ = x tan θ = x y csc θ = y 1 sec θ = x 1 cot θ = y x sin ( 9 0 ∘ − θ ) = x cos ( 9 0 ∘ − θ ) = y tan ( 9 0 ∘ − θ ) = y x csc ( 9 0 ∘ − θ ) = x 1 sec ( 9 0 ∘ − θ ) = y 1 cot ( 9 0 ∘ − θ ) = x y Using these equations, we can derive the cofunction identities by rewriting the equations in terms of θ \theta θ π 2 − θ \frac{\pi}{2} - \theta 2 π − θ
sin α = cos ( 9 0 ∘ − θ ) cos α = sin ( 9 0 ∘ − θ ) tan α = cot ( 9 0 ∘ − θ ) csc α = sec ( 9 0 ∘ − θ ) sec α = csc ( 9 0 ∘ − θ ) cot α = tan ( 9 0 ∘ − θ ) \begin{array}{lllllllll} \sin \alpha &=& \cos(90^\circ - \theta) \\[1em] \cos \alpha &=& \sin(90^\circ - \theta) \\[1em] \tan \alpha &=& \cot(90^\circ - \theta) \\[1em] \csc \alpha &=& \sec(90^\circ - \theta) \\[1em] \sec \alpha &=& \csc(90^\circ - \theta) \\[1em] \cot \alpha &=& \tan(90^\circ - \theta) \\[1em] \end{array} sin α cos α tan α csc α sec α cot α = = = = = = cos ( 9 0 ∘ − θ ) sin ( 9 0 ∘ − θ ) cot ( 9 0 ∘ − θ ) sec ( 9 0 ∘ − θ ) csc ( 9 0 ∘ − θ ) tan ( 9 0 ∘ − θ ) Sum of Sine Using the cofunction identities, we can rewrite sin ( α + β ) \sin(\alpha + \beta) sin ( α + β ) sin ( α + β ) = cos ( π 2 − ( α + β ) ) \sin(\alpha + \beta) = \cos(\frac{\pi}{2} - (\alpha + \beta)) sin ( α + β ) = cos ( 2 π − ( α + β ))
sin ( α + β ) = cos ( π 2 − ( α + β ) ) = cos ( π 2 − α − β ) = cos ( ( π 2 − α ) − β ) = cos ( π 2 − α ) cos β + sin ( π 2 − α ) sin β = sin α cos β + cos α sin β \begin{array}{cccccccc} \sin(\alpha + \beta) &=& \cos(\frac{\pi}{2} - (\alpha + \beta)) \\[1em] &=& \cos(\frac{\pi}{2} - \alpha - \beta) \\[1em] &=& \cos((\frac{\pi}{2} - \alpha) - \beta) \\[1em] &=& \cos(\frac{\pi}{2} - \alpha)\cos \beta + \sin(\frac{\pi}{2} - \alpha)\sin \beta \\[1em] &=& \sin \alpha \cos \beta + \cos \alpha \sin \beta \\[1em] \end{array} sin ( α + β ) = = = = = cos ( 2 π − ( α + β )) cos ( 2 π − α − β ) cos (( 2 π − α ) − β ) cos ( 2 π − α ) cos β + sin ( 2 π − α ) sin β sin α cos β + cos α sin β So, the derived formula for the sum of sine is sin ( α + β ) = sin α cos β + cos α sin β \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta sin ( α + β ) = sin α cos β + cos α sin β
Difference of Sine We can derive the difference formula for sine by using the sum of sine formula because sin ( α − β ) = sin ( α + ( − β ) ) \sin(\alpha - \beta) = \sin(\alpha + (-\beta)) sin ( α − β ) = sin ( α + ( − β ))
sin ( α − β ) = sin ( α + ( − β ) ) = sin α cos ( − β ) + cos α sin ( − β ) = sin α cos β + cos α ( − sin β ) = sin α cos β − cos α sin β \begin{array}{cccccccc} \sin(\alpha - \beta) &=& \sin(\alpha + (-\beta)) \\[1em] &=& \sin \alpha \cos(-\beta) + \cos \alpha \sin(-\beta) \\[1em] &=& \sin \alpha \cos \beta + \cos \alpha (-\sin \beta) \\[1em] &=& \sin \alpha \cos \beta - \cos \alpha \sin \beta \\[1em] \end{array} sin ( α − β ) = = = = sin ( α + ( − β )) sin α cos ( − β ) + cos α sin ( − β ) sin α cos β + cos α ( − sin β ) sin α cos β − cos α sin β So, the derived formula for the difference of sine is sin ( α − β ) = sin α cos β − cos α sin β \sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta sin ( α − β ) = sin α cos β − cos α sin β
Sum and Difference of Tangent Using the fact that tan θ = sin θ cos θ \tan \theta = \dfrac{\sin \theta}{\cos \theta} tan θ = cos θ sin θ
tan ( α + β ) = sin ( α + β ) cos ( α + β ) = sin α cos β + cos α sin β cos α cos β − sin α sin β = sin α cos β + cos α sin β cos α cos β ÷ cos α cos β − sin α sin β cos α cos β = ( sin α cos β cos α cos β + cos α sin β cos α cos β ) ÷ ( cos α cos β cos α cos β − sin α sin β cos α cos β ) = ( sin α cos α + sin β cos β ) ÷ ( 1 − sin α sin β cos α cos β ) = ( tan α + tan β ) ÷ ( 1 − tan α tan β ) = tan α + tan β 1 − tan α tan β \begin{array}{cccccccc} \tan(\alpha + \beta) &=& \dfrac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)} \\[1.5em] &=& \dfrac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin \beta} \\[1.5em] &=& \dfrac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta} \div \dfrac{\cos \alpha \cos \beta - \sin \alpha \sin \beta}{\cos \alpha \cos \beta} \\[1.5em] &=& (\dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta} + \dfrac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta}) \div (\dfrac{\cos \alpha \cos \beta}{\cos \alpha \cos \beta} - \dfrac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}) \\[1.5em] &=& (\dfrac{\sin \alpha}{\cos \alpha} + \dfrac{\sin \beta}{\cos \beta}) \div (1 - \dfrac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}) \\[1.5em] &=& (\tan \alpha + \tan \beta) \div (1 - \tan \alpha \tan \beta) \\[1.5em] &=& \dfrac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} \\[1.5em] \end{array} tan ( α + β ) = = = = = = = cos ( α + β ) sin ( α + β ) cos α cos β − sin α sin β sin α cos β + cos α sin β cos α cos β sin α cos β + cos α sin β ÷ cos α cos β cos α cos β − sin α sin β ( cos α cos β sin α cos β + cos α cos β cos α sin β ) ÷ ( cos α cos β cos α cos β − cos α cos β sin α sin β ) ( cos α sin α + cos β sin β ) ÷ ( 1 − cos α cos β sin α sin β ) ( tan α + tan β ) ÷ ( 1 − tan α tan β ) 1 − tan α tan β tan α + tan β So, the derived formula for the sum of tangent is tan ( α + β ) = tan α + tan β 1 − tan α tan β \tan(\alpha + \beta) = \dfrac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} tan ( α + β ) = 1 − tan α tan β tan α + tan β tan ( α − β ) = tan ( α + ( − β ) ) \tan(\alpha - \beta) = \tan(\alpha + (-\beta)) tan ( α − β ) = tan ( α + ( − β ))
tan ( α − β ) = tan ( α + ( − β ) ) = tan α + tan ( − β ) 1 − tan α tan ( − β ) = tan α + ( − tan β ) 1 − tan α ( − tan β ) = tan α − tan β 1 + tan α tan β \begin{array}{cccccccc} \tan(\alpha - \beta) &=& \tan(\alpha + (-\beta)) \\[1em] &=& \dfrac{\tan \alpha + \tan(-\beta)}{1 - \tan \alpha \tan(-\beta)} \\[1.5em] &=& \dfrac{\tan \alpha + (-\tan \beta)}{1 - \tan \alpha (-\tan \beta)} \\[1.5em] &=& \dfrac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} \\[1.5em] \end{array} tan ( α − β ) = = = = tan ( α + ( − β )) 1 − tan α tan ( − β ) tan α + tan ( − β ) 1 − tan α ( − tan β ) tan α + ( − tan β ) 1 + tan α tan β tan α − tan β So, the derived formula for the difference of tangent is tan ( α − β ) = tan α − tan β 1 + tan α tan β \tan(\alpha - \beta) = \dfrac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} tan ( α − β ) = 1 + tan α tan β tan α − tan β
Trigonometric Identities The cofunction identities are...
sin ( 9 0 ∘ − θ ) = cos θ cos ( 9 0 ∘ − θ ) = sin θ csc ( 9 0 ∘ − θ ) = sec θ sec ( 9 0 ∘ − θ ) = csc θ tan ( 9 0 ∘ − θ ) = cot θ cot ( 9 0 ∘ − θ ) = tan θ \begin{array}{ccccccccc} \sin(90^\circ - \theta) &=& \cos \theta &&& \cos(90^\circ - \theta) &=& \sin \theta \\[1em] \csc(90^\circ - \theta) &=& \sec \theta &&& \sec(90^\circ - \theta) &=& \csc \theta \\[1em] \tan(90^\circ - \theta) &=& \cot \theta &&& \cot(90^\circ - \theta) &=& \tan \theta \\[1em] \end{array} sin ( 9 0 ∘ − θ ) csc ( 9 0 ∘ − θ ) tan ( 9 0 ∘ − θ ) = = = cos θ sec θ cot θ cos ( 9 0 ∘ − θ ) sec ( 9 0 ∘ − θ ) cot ( 9 0 ∘ − θ ) = = = sin θ csc θ tan θ and the sum and difference identities are...
sin ( α + β ) = sin α cos β + cos α sin β sin ( α − β ) = sin α cos β − cos α sin β cos ( α + β ) = cos α cos β − sin α sin β cos ( α − β ) = cos α cos β + sin α sin β tan ( α + β ) = tan α + tan β 1 − tan α tan β tan ( α − β ) = tan α − tan β 1 + tan α tan β \begin{array}{ccccccccc} \sin(\alpha + \beta) &=& \sin \alpha \cos \beta + \cos \alpha \sin \beta \\[1.5em] \sin(\alpha - \beta) &=& \sin \alpha \cos \beta - \cos \alpha \sin \beta \\[1.5em] \cos(\alpha + \beta) &=& \cos \alpha \cos \beta - \sin \alpha \sin \beta \\[1.5em] \cos(\alpha - \beta) &=& \cos \alpha \cos \beta + \sin \alpha \sin \beta \\[1.5em] \tan(\alpha + \beta) &=& \dfrac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} \\[1.5em] \tan(\alpha - \beta) &=& \dfrac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} \\[1.5em] \end{array} sin ( α + β ) sin ( α − β ) cos ( α + β ) cos ( α − β ) tan ( α + β ) tan ( α − β ) = = = = = = sin α cos β + cos α sin β sin α cos β − cos α sin β cos α cos β − sin α sin β cos α cos β + sin α sin β 1 − tan α tan β tan α + tan β 1 + tan α tan β tan α − tan β