Power and Polynomial Functions

Linear, quadratic, and cubic functions are all types of polynomials. This means all properties of polynomials are shared by these functions and so having a deep understanding of polynomials is invaluable.

Power Functions

A power function is a function with a single term that is the product of a real number which is the coefficient and a variable raised to a fixed real number. In other words, a power function is a function that can be represented in the form, $f(x) = kx^p$ where $k$ and $p$ are real numbers and $k$ is the coefficient.

End behavior describes how functions behaves as it approaches positive or negative infinity. Let $f(x)$ be a positive even-power function like $x^2$ and $x^4$. Then as $x$ approaches positive or negative infinity, $f(x)$ increases without bound which means $f(x)$ approaches infinity. Using the symbol $\to$ which means approaches, we get the symbolic form: as $x \to \pm \infty, f(x) \to \infty$.

On the other hand, let $f(x)$ be a positive odd-power function. Then as $x$ approaches positive infinity, $f(x)$ increases without bound. But, as $x$ approaches negative infinity, $f(x)$ decreases without bound. In symbolic form we get, as $x \to \infty, f(x) \to \infty$ and as $x \to -\infty, f(x) \to -\infty$.

Finally, let $f(x)$ be a negative power function instead. If it is even-powered then as $x \to \pm \infty, f(x) \to -\infty$. Otherwise, if it is odd-powered then as $x \to \infty, f(x) \to -\infty$ and as $x \to -\infty, f(x) \to \infty$.

Fig. 1 - End Behavior

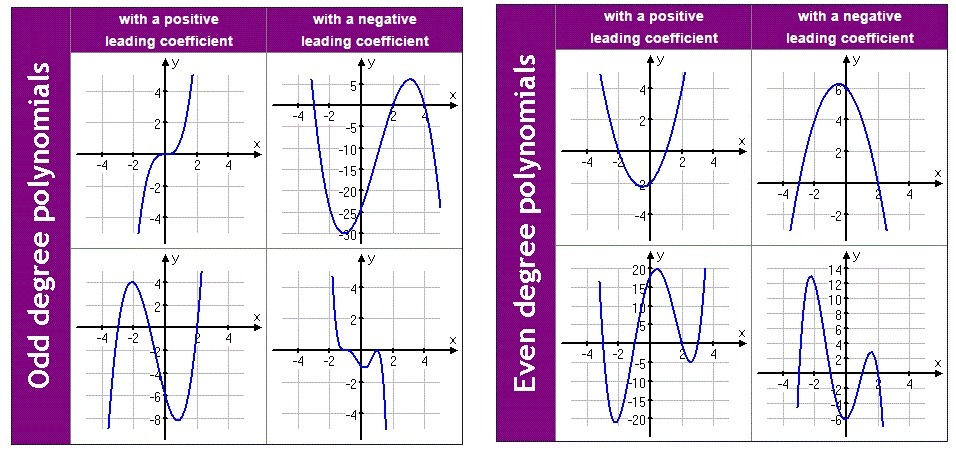
Polynomial Functions

A polynomial function is a function that can be written in the form $f(x) = a_nx^n + ... + a_2x^2 + a_1x + a_0$ where $n$ is a non-negative integer. Also note that each $a_i$ is a coefficient and can be any real number but $a_n \neq 0$. This means that each expression $a_ix^i$ is a term of a polynomial function.

note

The form $f(x) = a_nx^n + ... + a_2x^2 + a_1x + a_0$ is the general form of a polynomial.

There are a few parts of a polynomial that we use often to analyze or predict the behaviors of the function...

1. The degree is the highest power in the polynomial.
2. The leading term is the term containing the highest power.
3. The leading coefficient is the coefficient of the leading term.

The end behavior of a polynomial is impacted by the leading term because it is the term with the highest power. This means the term will grow significantly faster than the other terms as $x$ gets very large or very small essentially causing the leading term to dominate the graph. Due to this fact, the end behavior of a polynomial function will match the end behavior of the power function consisting of the leading term. For example, we can obtain the end behavior of $f(x) = 3x^3 + 2x^2 + 1$ through the power function $f(x) = 3x^3$.

Local Behavior

Local behavior is the behavior of the function in a small region or the "middle". Local behavior includes the intercepts. The $x$-intercept can be found by solving for $f(x) = 0$ and the $y$-intercept can be found by setting $x = 0$ to solve for $f(x)$. The local behavior also includes the turning points of a graph which are the points at which the graph changes directions from increasing to decreasing or decreasing to increasing. Using these points, we can analyze the local behavior of any function.

Finally, we are able to determine the number of $x$-intercepts and turning points of a polynomial function solely based on its degree. A polynomial function of $n$th degree is a product of $n$ factors and so it will have at most $n$ $x$-intercepts and $n - 1$ turning points.

note

All polynomial functions are continuous functions meaning they have no breaks in their graphs. This means their graph can be drawn without lifting the pen from the paper.

All these functions also have smooth curves which means their graphs has no sharp corners. This causes the turning points to always occur at rounded curves.