Inverse Trigonometric Functions

Through the use of trigonometric functions, we can find the ratio of sides of a right triangle given an angle. However, it is often useful and necessary to be able to find the angle given the ratio of sides. This is where inverse trigonometric functions come into play.

Inverse Sine, Cosine, and Tangent

The inverse function "undoes" what the original function "does". However, only one-to-one functions can be inverted because we swap the domain and range between the two functions meaning the original function must pass the horizontal line test for the inverse to pass the vertical line test.

Inherently, the sine, cosine, and tangent functions are not one-to-one function as they would fail the horizontal line test. In fact, no periodic function can be one-to-one because each output in its range corresponds to at least one input in every period and there are infinitely many periods. To remedy this, we restrict the domain of each function to yield a new function that is one-to-one that can be inverted. These domain restrictions are somewhat arbitrary, but the conventional choices are as follows...

• $\text{Sine: } [-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$
• $\text{Cosine: } [0, \pi]$
• $\text{Tangent: } (-\dfrac{\pi}{2}, \dfrac{\pi}{2})$

Using these restrictions, we can define the inverse functions as follows:

• The inverse sine function is defined as $\sin^{-1}(x)$ or $\arcsin(x)$ which means $x = \sin(y)$. This function is sometimes called the arc sine function. Also note that $y = \sin^{-1}(x)$ has domain $[-1, 1]$ and range $[-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$.
• The inverse cosine function is defined as $\cos^{-1}(x)$ or $\arccos(x)$ which means $x = \cos(y)$. This function is sometimes called the arc cosine function. Also note that $y = \cos^{-1}(x)$ has domain $[-1, 1]$ and range $[0, \pi]$.
• The inverse tangent function is defined as $\tan^{-1}(x)$ or $\arctan(x)$ which means $x = \tan(y)$. This function is sometimes called the arc tangent function. Also note that $y = \tan^{-1}(x)$ has domain $(-\infty, \infty)$ and range $(-\dfrac{\pi}{2}, \dfrac{\pi}{2})$.

note

The inverse of any function can be found by reflecting the original function across the line $y = x$. This means that $y = \sin^{-1}(x)$ is the reflection of $y = \sin(x)$ across the line $y = x$. This is true for all inverse functions.

Also note that the notation $\sin^{-1}(x)$ is not the same as $\dfrac{1}{\sin(x)}$. The latter is the cosecant function, which is defined as $\csc(x) = \dfrac{1}{\sin(x)}$ or $(\sin(x))^{-1}$. The notation $\sin^{-1}(x)$ is reserved for the inverse sine function.

Finding Exact Values

Just as we did with the original trigonometric functions, we can give exact values for the inverse functions when we are using the special angles, specifically $0, \dfrac{\pi}{6}, \dfrac{\pi}{4}, \dfrac{\pi}{3}, \dfrac{\pi}{2}$, and their reflections into other quadrants.

Given a "special angle" input value, we can evalue an inverse trigonometric function by finding angle $x$ such that the original trigonometric function has an output equal to the given input for the inverse trigonometric function. In the case that $x$ is not defined in the range of the inverse function, we find another angle $y$ such that the angle $y$ is in the defined range of the inverse trigonometric function.

$\underline{Example}$

Evalue $\cos^{-1}(\dfrac{1}{2})$.

The cosine function is positive in the first and fourth quadrants but the range of the inverse cosine function is $[0, \pi]$. Therefore, we need to find an angle in the first quadrant that has a cosine value of $\dfrac{1}{2}$. This angle is $\dfrac{\pi}{3}$.

The solution is $\cos^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{3}$.

Composite Functions

As a refresher, a composite function is a function that is formed by combining two or more functions. The notation for a composite function is $f(g(x))$ which means that we first apply the function $g(x)$ and then apply the function $f(x)$ to the result of $g(x)$. The order of the functions matters, so $f(g(x)) \neq g(f(x))$ in general.

There are four cases to consider when dealing with trigonometric functions and their inverses. The first case is when the composition is of the form $f(f^{-1}(x))$...

• $\sin(\sin^{-1}(x)) = x \:\text{ for }\: -1 \leq x \leq 1$
• $\cos(\cos^{-1}(x)) = x \:\text{ for }\: 0 \leq x \leq 1$
• $\tan(\tan^{-1}(x)) = x \:\text{ for }\: -\infty < x < \infty$

For all trigonometric functions, the composition of the function and its inverse is equal to the input value. This is the same for the next case where the composition is of the form $f^{-1}(f(x))$...

• $\sin^{-1}(\sin(x)) = x \:\text{ only for }\: -\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}$
• $\cos^{-1}(\cos(x)) = x \:\text{ only for }\: 0 \leq x \leq \pi$
• $\tan^{-1}(\tan(x)) = x \:\text{ only for }\: -\dfrac{\pi}{2} < x < \dfrac{\pi}{2}$

note

We have to be careful with composition because $\sin^{-1}(\sin(x)) \neq x$ because this is not true for all values of $x$. The domain has to be restricted to the range of the inverse for the composition to be equal to the input value. This is the same for the other trigonometric functions as well.

Different Functions

The third case is when the composition is of the form $f^{-1}(g(x))$ where both functions are trigonometric functions but not the same functions. For special values of $x$, we can exactly evaluate the inner function and then the outer function to find the value of the composition. This is a good approach however we can find a more general approach using a right triangle.

Fig. 1 - Right Triangle Composition

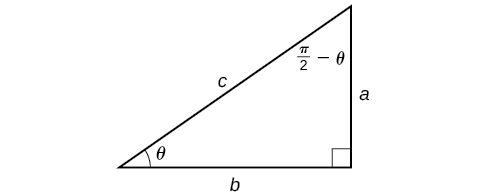
Consider the relation between two acute angles of a right triangle where one is $\theta$ making the other one $\dfrac{\pi}{2} - \theta$. Using the fact that $\cos \theta = \dfrac{b}{c} = \sin(\dfrac{\pi}{2} - \theta)$, we can deduce that $\sin^{-1}(\cos \theta) = \dfrac{\pi}{2} - \theta$. Similarly, based on $\sin \theta = \dfrac{a}{c} = \cos(\dfrac{\pi}{2} - \theta)$, we can deduce that $\cos^{-1}(\sin \theta) = \dfrac{\pi}{2} - \theta$. This means that the composition of the sine and cosine functions is equal to the complementary angle of the original angle.

Using these new relations, given functions of the form $\sin^{-1}(\cos(x))$ or $\cos^{-1}(\sin(x))$, we can evaluate the composition as follows:

1. If $x \in [0, \pi]$, then $\sin^{-1}(\cos(x)) = \dfrac{\pi}{2} - x$.
2. If $x \notin [0, \pi]$, then find another angle $y$ in $[0, \pi]$ such that $\cos(y) = \cos(x)$. Then follow the first step.
3. If $x \in [-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$, then $\cos^{-1}(\sin(x)) = \dfrac{\pi}{2} - x$.
4. If $x \notin [-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$, then find another angle $y$ in $[-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$ such that $\sin(y) = \sin(x)$. Then follow the third step.

$\underline{Example}$

Evaluate $\cos^{-1}(\sin(-\dfrac{11\pi}{4}))$.

For the form $\cos^{-1}(\sin(x))$, we need $x$ to be in the range $[-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$. In this case, the angle is $-\dfrac{11\pi}{4}$ which is not in the range and so we need to find another angle $y$ such that $\sin(y) = \sin(-\dfrac{11\pi}{4})$ and $y \in [-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$.

The angle $-\dfrac{11\pi}{4}$ is coterminal with $-\dfrac{3\pi}{4}$ which is in the third quadrant. Next, the reference angle of $\dfrac{3\pi}{4}$ is $\dfrac{\pi}{4}$. Combining this with the fact that sine is negative in the third quadrant, we can find the angle $y = -\dfrac{\pi}{4}$.

Now that we have an angle in the range of $[-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$, we can use the relation $\cos^{-1}(\sin(x)) = \dfrac{\pi}{2} - x$ to find the value of the composition.

$\cos^{-1}(\sin(-\dfrac{11\pi}{4})) = \dfrac{\pi}{2} - x = \dfrac{\pi}{2} - (-\dfrac{\pi}{4}) = \dfrac{\pi}{2} + \dfrac{\pi}{4} = \dfrac{3\pi}{4}$.

The solution is $\cos^{-1}(\sin(-\dfrac{11\pi}{4})) = \dfrac{3\pi}{4}$.

Finally, the last form of composition is $f(g^{-1}(x))$ where both functions are trigonometric functions but not the same functions. In this case, we can use the pythagorean identities like $\sin^2(x) + \cos^2(x) = 1$ and our knowledge with trigonometric functions to find the value of the composition.

$\underline{Example}$

Evaluate $\cos(\sin^{-1}(\dfrac{7}{9}))$.

Starting with the inside, we can state there exists an angle $\theta$ such that $\sin^{-1}(\dfrac{7}{9}) = \theta$ which means $\sin \theta = \dfrac{7}{9}$. Using the pythagorean identity, we can find the cosine value of the angle $\theta$.

$$\begin{array}{llllllllll} \sin^2 \theta + \cos^2 \theta &=& 1 \\[0.5em] (\frac{7}{9})^2 + \cos^2 \theta &=& 1 \\[0.5em] \frac{49}{81} + \cos^2 \theta &=& 1 \\[0.5em] \cos^2 \theta &=& 1 - \frac{49}{81} \\[0.5em] \cos^2 \theta &=& \frac{32}{81} \\[0.5em] \cos \theta &=& \frac{4\sqrt{2}}{9} \\[0.5em] \end{array}$$

Since $\theta = \sin^{-1}(\dfrac{7}{9})$ is in the first quadrant, $\cos \theta$ is positive. Therefore, we can conclude that $\cos(\sin^{-1}(\dfrac{7}{9})) = \dfrac{4\sqrt{2}}{9}$.

The solution is $\cos(\sin^{-1}(\dfrac{7}{9})) = \dfrac{4\sqrt{2}}{9}$.