Graphs
Graphs are similar to trees infact all trees are graphs but all graphs are not trees. This is because graphs have two properties that trees do not. Firstly, they can have more than one arrow that lead into some nodes. Secondly, they can have arrows that lead back into themselves which we call cycles.
Directed Cyclic Graphs
Graphs come in many forms, they can be directed or undirected. Directed graphs have arrows that point in a specific direction while undirected graphs have arrows that point in both directions. If the graph has cycles then it is called a cyclic graph, otherwise it is called an acyclic graph. We will be focusing on directed cyclic graphs in this section which are graphs that have arrows that point in a specific direction and have cycles.
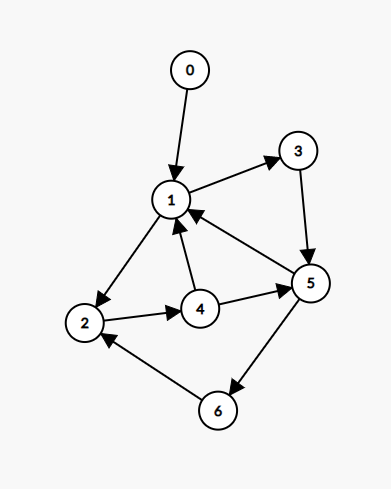
In Figure 1, there are many cycles in the graph including the cycle 1 -> 2 -> 4 -> 1 and the cycle 3 -> 5 -> 1 -> 3. The graph is also directed because the arrows point in a specific direction.
Shared
To be able to create cycles in our graphs, we need a new primitive called shared because it allows us bind expressions to an id so that we can reference it later in the body.
The syntax for shared is (shared ([<id> <expression>] ...) <body>).
(shared (-A- (cons 1 -B-))
(-B- 7)
-A-)
; The above expression is equivalent to
(cons 1 7)
Data Definition
Now that we have the primitive shared, we can create a data definition for graphs, one that is able to create cycles.
(define-struct node (name exits))
;; Node is (make-node String (listof Node))
;; interp. a node's name, and list of nodes that the exit leads to
; Only A leads to B
(define N1 (make-node "A" (list (make-node "B" empty))))
; A cycle between A and B
(define N2 (shared ([-A- (make-node "A" (list -B-))]
[-B- (make-node "B" (list -A-))])
-A-))
; A cycle between A, B, and C
(define N3 (shared ([-A- (make-node "A" (list -B-))]
[-B- (make-node "B" (list -C-))]
[-C- (make-node "C" (list -A-))])
-A-))
; A more complex graph
(define N4
(shared ([-A- (make-room "A" (list -B- -D-))]
[-B- (make-room "B" (list -C- -E-))]
[-C- (make-room "C" (list -B-))]
[-D- (make-room "D" (list -E-))]
[-E- (make-room "E" (list -F- -A-))]
[-F- (make-room "F" (list))])
-A-))
Template
Our template needs to be a blend of structural recursion that is encapsulated with local and is tail-recursive with a worklist. It also will need a context-preserving accumulator which keeps track of all the nodes we have already visited.
The template is similar to the template for an arbitrary tree except that we need to keep track of the nodes we have already visited so that we do not get stuck in a cycle which would cause our program to run forever.
(define (fn-for-graph n0)
;; todo is (listof Node) ; a worklist accumulator
;; visited is (listof String) ; context preserving accumulator, names of rooms already visited
;; ASSUME: Every node has an unique name
(local [(define (fn-for-node n todo visited)
(if (member (node-name n) visited)
(fn-for-lon todo visited)
(fn-for-lon (append (node-exits n) todo)
(cons (node-name n) visited))))
(define (fn-for-lon todo visited)
(cond [(empty? todo) (...)]
[else
(fn-for-node (first todo)
(rest todo)
visited)]))]
(fn-for-node n0 empty empty)))
Reachable?
Let's use our template to create a function that determines if a node is reachable from another node. It could also be considered a function that determines if a node is in a graph.
;; Node String -> Boolean
;; produce true if starting at n0 it is possible to reach a node with the name nme.
#;
(define (reachable? n0 nme) false) ; stub
(check-expect (reachable? N1 "A") true)
(check-expect (reachable? N1 "B") true)
(check-expect (reachable? N1 "C") false)
(check-expect (reachable? (first (node-exits N1)) "A") false)
(check-expect (reachable? N4 "F") true)
(define (reachable? n0 nme)
;; todo is (listof Node) ; a worklist accumulator
;; visited is (listof String) ; context preserving accumulator, names of nodes already visited
(local [(define (fn-for-node n todo visited)
(cond [(string=? (node-name n) nme) true]
[(member (node-name n) visited) (fn-for-lon todo visited)]
[else (fn-for-lon (append (node-exits n) todo)
(cons (node-name n) visited))]))
(define (fn-for-lon todo visited)
(cond [(empty? todo) false]
[else
(fn-for-node (first todo)
(rest todo)
visited)]))]
(fn-for-node n0 empty empty)))