Sudoku
Sudoku is a popular logic puzzle where the objective is to fill a 9 x 9 grid with digits so that each column, each row, and each of the boxes contain digits from 1 - 9 with no repeats in each.
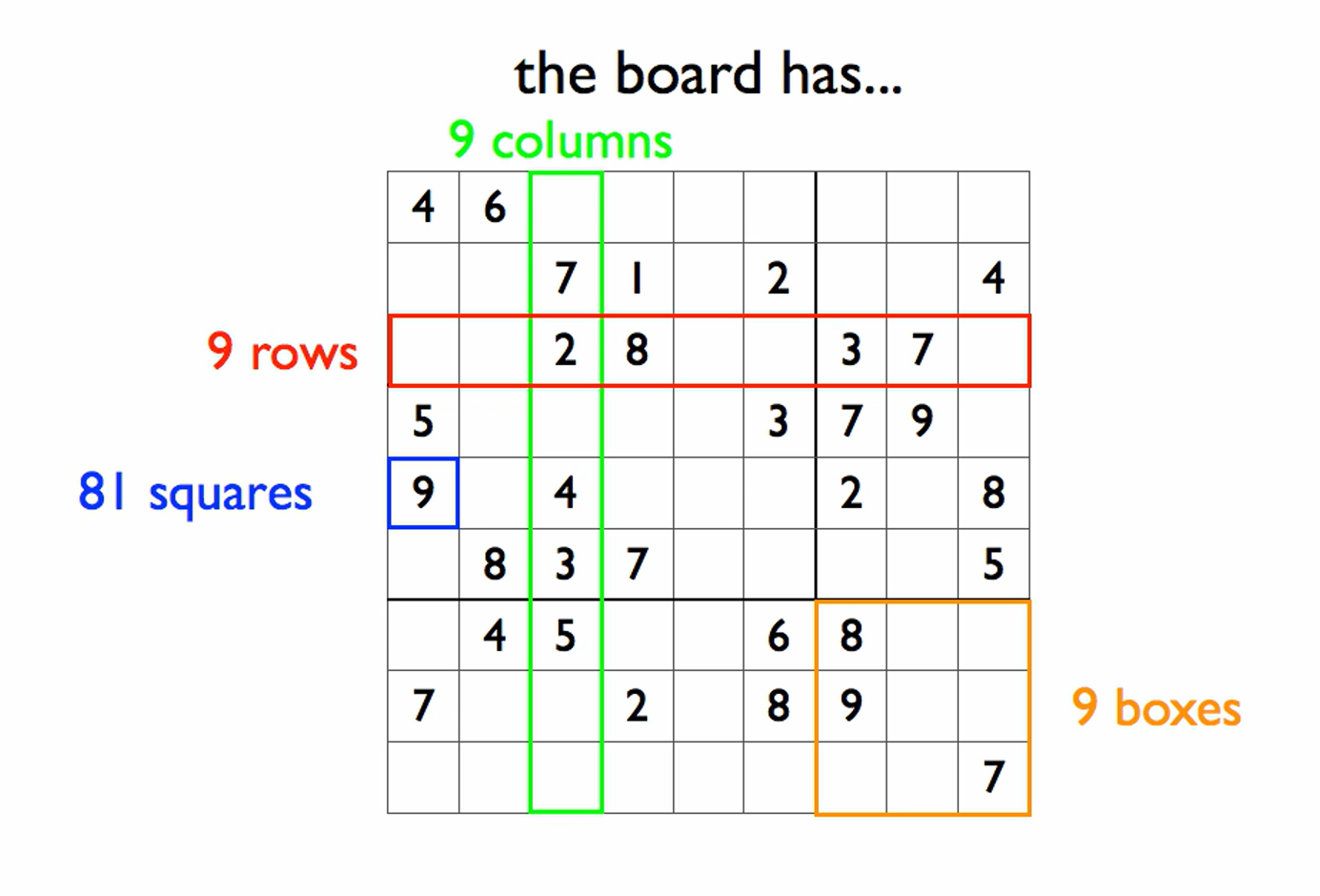
The program we are creating is a Sudoku solver that uses brute force (testing every combination) to solve any legal sudoku board given.
Data Definitions
Before we can create the program, we need to make some data definitions to interpret what a sudoku board is. A board is comprised of 81 cells that are either empty or have a value.
;; Val is Natural[1, 9]
;; Board is (listof Val|false) that is 81 elements long
;; interp.
;; Visually a board that is a 9x9 array of squares, where each square
;; has a row and column number. But we represent it as a
;; single flast list, in which the rows are layed out one after
;; another in linear fashion.
Now that we have a board, we need to be able to reference a specific cell of the board at anytime so that we can read and change it.
;; Pos is Natural[0, 80]
;; interp.
;; the position of a square on the board, for a given p, then
;; - the row is (quotient p 9)
;; - the column is (remainder p 9)
Finally, the last data definition that will come in handy are the units (rows, columns, and boxes). This will be useful later on for checking if all the units are valid and don't break the rule.
Constants
We mainly need boards as constants so that we can use them for tests later.
(define B false) ;B stands for blank
(define BD1
(list B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B))
(define BD2
(list 1 2 3 4 5 6 7 8 9
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B))
(define BD3
(list 1 B B B B B B B B
2 B B B B B B B B
3 B B B B B B B B
4 B B B B B B B B
5 B B B B B B B B
6 B B B B B B B B
7 B B B B B B B B
8 B B B B B B B B
9 B B B B B B B B))
(define BD4 ;easy
(list 2 7 4 B 9 1 B B 5
1 B B 5 B B B 9 B
6 B B B B 3 2 8 B
B B 1 9 B B B B 8
B B 5 1 B B 6 B B
7 B B B 8 B B B 3
4 B 2 B B B B B 9
B B B B B B B 7 B
8 B B 3 4 9 B B B))
(define BD4s ;solution to 4
(list 2 7 4 8 9 1 3 6 5
1 3 8 5 2 6 4 9 7
6 5 9 4 7 3 2 8 1
3 2 1 9 6 4 7 5 8
9 8 5 1 3 7 6 4 2
7 4 6 2 8 5 9 1 3
4 6 2 7 5 8 1 3 9
5 9 3 6 1 2 8 7 4
8 1 7 3 4 9 5 2 6))
(define BD5 ;hard
(list 5 B B B B 4 B 7 B
B 1 B B 5 B 6 B B
B B 4 9 B B B B B
B 9 B B B 7 5 B B
1 8 B 2 B B B B B
B B B B B 6 B B B
B B 3 B B B B B 8
B 6 B B 8 B B B 9
B B 8 B 7 B B 3 1))
(define BD5s ;solution to 5
(list 5 3 9 1 6 4 8 7 2
8 1 2 7 5 3 6 9 4
6 7 4 9 2 8 3 1 5
2 9 6 4 1 7 5 8 3
1 8 7 2 3 5 9 4 6
3 4 5 8 9 6 1 2 7
9 2 3 5 4 1 7 6 8
7 6 1 3 8 2 4 5 9
4 5 8 6 7 9 2 3 1))
(define BD6 ;hardest ever? (Dr Arto Inkala)
(list B B 5 3 B B B B B
8 B B B B B B 2 B
B 7 B B 1 B 5 B B
4 B B B B 5 3 B B
B 1 B B 7 B B B 6
B B 3 2 B B B 8 B
B 6 B 5 B B B B 9
B B 4 B B B B 3 B
B B B B B 9 7 B B))
(define BD7 ; no solution
(list 1 2 3 4 5 6 7 8 B
B B B B B B B B 2
B B B B B B B B 3
B B B B B B B B 4
B B B B B B B B 5
B B B B B B B B 6
B B B B B B B B 7
B B B B B B B B 8
B B B B B B B B 9))
We also need constants of all the 27 units on the board. This refers to the positions of the 9 columns, 9 rows, and 9 boxes on every board.
(define ROWS
(list (list 0 1 2 3 4 5 6 7 8)
(list 9 10 11 12 13 14 15 16 17)
(list 18 19 20 21 22 23 24 25 26)
(list 27 28 29 30 31 32 33 34 35)
(list 36 37 38 39 40 41 42 43 44)
(list 45 46 47 48 49 50 51 52 53)
(list 54 55 56 57 58 59 60 61 62)
(list 63 64 65 66 67 68 69 70 71)
(list 72 73 74 75 76 77 78 79 80)))
(define COLS
(list (list 0 9 18 27 36 45 54 63 72)
(list 1 10 19 28 37 46 55 64 73)
(list 2 11 20 29 38 47 56 65 74)
(list 3 12 21 30 39 48 57 66 75)
(list 4 13 22 31 40 49 58 67 76)
(list 5 14 23 32 41 50 59 68 77)
(list 6 15 24 33 42 51 60 69 78)
(list 7 16 25 34 43 52 61 70 79)
(list 8 17 26 35 44 53 62 71 80)))
(define BOXES
(list (list 0 1 2 9 10 11 18 19 20)
(list 3 4 5 12 13 14 21 22 23)
(list 6 7 8 15 16 17 24 25 26)
(list 27 28 29 36 37 38 45 46 47)
(list 30 31 32 39 40 41 48 49 50)
(list 33 34 35 42 43 44 51 52 53)
(list 54 55 56 63 64 65 72 73 74)
(list 57 58 59 66 67 68 75 76 77)
(list 60 61 62 69 70 71 78 79 80)))
(define UNITS (append ROWS COLS BOXES))
Functions
To solve a given sudoku board using brute force, we need to find the next empty position and try all the possible values from 1 to 9. We can keep repeating this for all the boards and removing all the boards that become invalid like if there are two duplicates in the same column. Using this method, we should end up with a valid solution where all the numbers work.
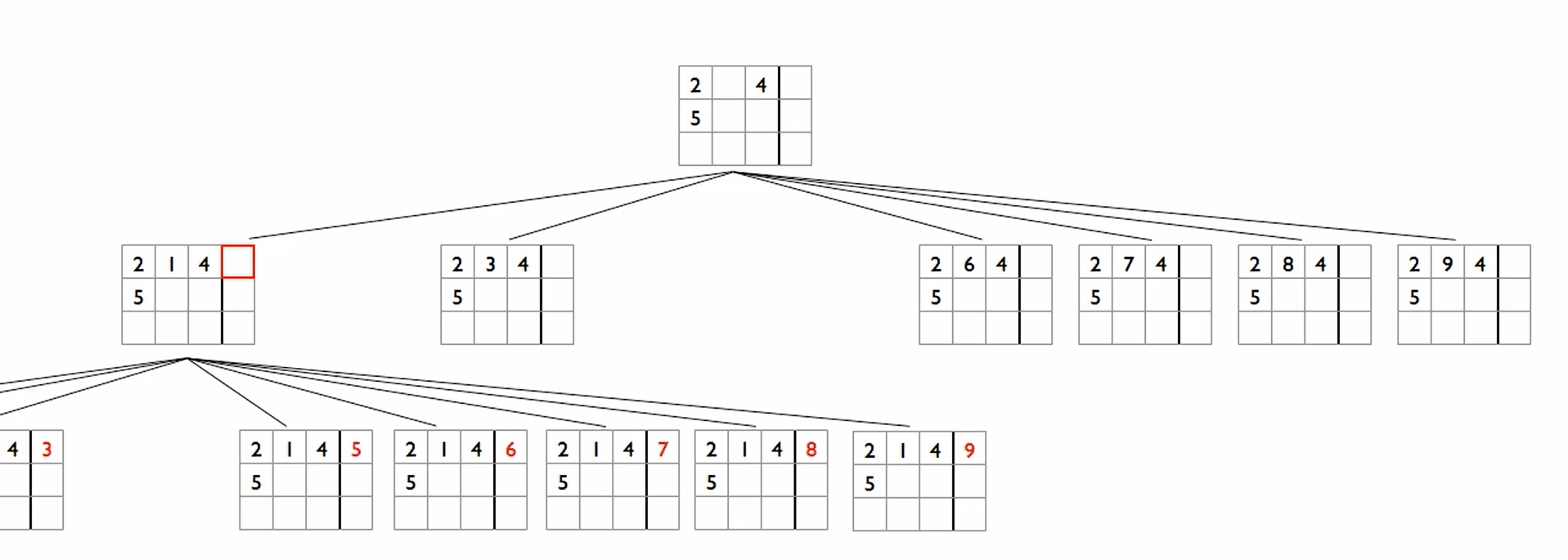
Our algorithm as seen above generates an arbitrary-arity tree and doing backtracking search over it in order to prune the invalid boards.
Template Blending
We want to begin with an arbitrary arity tree template because that is the data structure our algorithm is working with. Each branch can have anywhere between 0 to 9 valid boards and we do not know how deep the tree is.
;; Board -> Board or false
;; produce a solution for bd; or false if bd is unsolvable
;; Assume: bd is valid
#;
(define (solve bd) false) ; stub
(check-expect (solve BD4) BD4s)
(check-expect (solve BD5) BD5s)
(check-expect (solve BD7) false)
(define (solve bd)
(local [(define (solve--bd bd)
(... (solve--lobd (bd-subs bd))))
(define (solve--lobd lobd)
(cond [(empty? lobd) (...)]
[else
(... (solve--bd (first lobd))
(solve--lobd (rest lobd)))]))]
(solve--bd bd)))
Now we can work around the current template and blend in generative recursion. We want to generate a new set of valid boards during each iteration. Due to the complexity, we will use helpers and focus on the bigger picture here. We will need solved? which will tell us if the board is full meaning the solved board has been found causing us to return it. We will also need next-boards to take our current board and return a list of valid boards.
(define (solve bd)
(local [(define (solve--bd bd)
(if (solved? bd)
bd
(solve--lobd (next-boards bd))))
(define (solve--lobd lobd)
(cond [(empty? lobd) (...)]
[else
(... (solve--bd (first lobd))
(solve--lobd (rest lobd)))]))]
(solve--bd bd)))
The last step is to go through all the boards using backtracking search and make sure there are still valid boards left in the branch. If there are no valid boards left in the current branch, we need to look at a different branch.
(define (solve bd)
(local [(define (solve--bd bd)
(if (solved? bd)
bd
(solve--lobd (next-boards bd))))
(define (solve--lobd lobd)
(cond [(empty? lobd) false]
[else
(local [(define try (solve--bd (first lobd)))]
(if (not (false? try))
try
(solve--lobd (rest lobd))))]))]
(solve--bd bd)))
Position Functions
Before we continue on working on our helper functions, we need functions to help us manipulate the board. The first function we want is to be able to read the value in whatever position on the board.
(require racket/list)
;; Board Pos -> Val or false
;; Produce value at given position on board.
(check-expect (read-square BD2 5) 6)
(check-expect (read-square BD3 63) 8)
(define (read-square bd p)
(list-ref bd p))
We are using a new library using (require racket/list) to code these functions faster. They are not necessary but they definitely make it easier to code. This library provides list-ref which takes a list and a position and returns the value in that position. The library also includes take which takes a list and position and returns all the elements in the list up to the position. Finally, it also includes drop which takes a list and a position and returns a new list of all the elements in that position till the end of the list.
Our second function needs to be able to edit a value using a position and we will do this using the take and drop functions.
;; Board Pos Val -> Board
;; produce new board with val at given position
(check-expect (fill-square BD1 0 1)
(cons 1 (rest BD1)))
(define (fill-square bd p nv)
(append (take bd p)
(list nv)
(drop bd (add1 p))))
Generating Boards
Our first goal is to generate a new set of boards by filling the next empty position from 1 to 9. After this is done, we need to remove all the invalid boards leaving only valid boards generated. Due to the fact, this is a complex task, we can use function composition and solve each problem individually.
;; Board -> (listof Board)
;; produce list of valid next boards from board
;; finds first empty square, fills it with Natural[1, 9], keeps only valid boards
#;
(define (next-boards bd) empty) ; stub
(check-expect (next-boards (cons 1 (rest BD1)))
(list (cons 1 (cons 2 (rest (rest BD1))))
(cons 1 (cons 3 (rest (rest BD1))))
(cons 1 (cons 4 (rest (rest BD1))))
(cons 1 (cons 5 (rest (rest BD1))))
(cons 1 (cons 6 (rest (rest BD1))))
(cons 1 (cons 7 (rest (rest BD1))))
(cons 1 (cons 8 (rest (rest BD1))))
(cons 1 (cons 9 (rest (rest BD1))))))
(define (next-boards bd)
(keep-only-valid (fill-with-1-9 (find-blank bd) bd)))
Our first step is to find the first blank position which we can do by searching the list till we find the first false. Each time we go deeper into the list, the position increases by 1 till we arrive to our position.
;; Board -> Pos
;; produces the position of the first blank square
;; Assume: the board has at least one blank square
#;
(define (find-blank bd) 0) ; stub
(check-expect (find-blank BD1) 0)
(check-expect (find-blank (cons 2 (rest BD1))) 1)
(check-expect (find-blank (cons 2 (cons 4 (rest (rest BD1))))) 2)
(define (find-blank bd)
(cond [(empty? bd) (error "The board didn't have a blank space.")]
[else
(if (false? (first bd))
0
(+ 1 (find-blank (rest bd))))]))
Now that we have the position we need to fill, we need to generate 9 different boards by changing what value goes in that empty cell. We can do this by using build-list which is a built-in function that allows us to create lists.
;; Pos Board -> (listof Board)
;; produce 9 boards, with blank filled with Natural[1, 9]
#;
(define (fill-with-1-9 p bd) empty) ; stub
(check-expect (fill-with-1-9 0 BD1)
(list (cons 1 (rest BD1))
(cons 2 (rest BD1))
(cons 3 (rest BD1))
(cons 4 (rest BD1))
(cons 5 (rest BD1))
(cons 6 (rest BD1))
(cons 7 (rest BD1))
(cons 8 (rest BD1))
(cons 9 (rest BD1))))
(define (fill-with-1-9 p bd)
(local [(define (build-one n)
(fill-square bd p (+ n 1)))]
(build-list 9 build-one)))
The last step to completing our board generator is to remove all the boards that are not valid which can be done using filter.
;; (listof Board) -> (listof Board)
;; produce list containing only valid boards
#;
(define (keep-only-valid lobd) empty) ; stub
(check-expect (keep-only-valid (list (cons 1 (cons 1 (rest (rest BD1))))))
empty)
(define (keep-only-valid lobd)
(filter valid-board? lobd))
Pruning Boards
As you can see, we still need valid-board? in order to get the next-boards function working. Figuring out if a board is valid is the most difficult task. We know a board is valid when every position in every unit on the board has no values that are repeating.
;; Board -> Boolean
;; produce true if board is valid, false otherwise
;; valid means no unit on the board has the same value twice; false otherwise
#;
(define (valid-board? bd) false)
(check-expect (valid-board? BD1) true)
(check-expect (valid-board? BD2) true)
(check-expect (valid-board? BD3) true)
(check-expect (valid-board? BD4) true)
(check-expect (valid-board? BD5) true)
(check-expect (valid-board? (cons 2 (rest BD2))) false)
(check-expect (valid-board? (cons 2 (rest BD3))) false)
(check-expect (valid-board? (fill-square BD4 1 6)) false)
(define (valid-board? bd)
(local [; Is true only if all the units are valid
(define (valid-units? lou)
(andmap valid-unit? lou))
; Gets the values from a unit keeping only the numbers and checks for duplicates.
; If there is a duplicate, this function returns false because it is not valid.
(define (valid-unit? u)
(no-duplicates?
(keep-only-values
(read-unit u))))
; Maps each position in a unit to its cooresponding value
(define (read-unit u)
(map read-pos u))
; Returns the value from a given position (used to map)
(define (read-pos p)
(read-square bd p))
; Only keeps the numbers in a unit by using filter
(define (keep-only-values lovf)
(filter number? lovf))
; Is true if the no duplicates
(define (no-duplicates? lov)
(cond [(empty? lov) true]
[else
(if (member (first lov) (rest lov))
false
(no-duplicates? (rest lov)))]))]
(valid-units? UNITS)))
The function no-duplicates? uses member which checks if a value is in a list. If the first value appears in the rest of the list, this meant we found a duplicate. If it didn't we just needed to check the rest of the list until no values are left in the list.
Checking for Solutions
We have been making sure that during generation, only valid boards are placed in the tree so that means a solved board is one that is full. If every value in the board is a number, then we know its full meaning the board has been solved.
;; Board -> Boolean
;; produce true if board is solved
;; Assume: board is valid, so it is solved if it is full
#;
(define (solved? bd) false) ; stub
(check-expect (solved? BD1) false)
(check-expect (solved? BD2) false)
(check-expect (solved? BD4s) true)
(define (solved? bd)
(andmap number? bd))
Completed Program
We completed our brute force sudoku solver! Here is the complete program...
(require racket/list)
;; ======================================
;; Data Definition:
;; Val is Natural[1, 9]
;; Board is (listof Val|false) that is 81 elements long
;; interp.
;; Visually a board that is a 9x9 array of squares, where each square
;; has a row and column number. But we represent it as a
;; single flast list, in which the rows are layed out one after
;; another in linear fashion.
;; Pos is Natural[0, 80]
;; interp.
;; the position of a square on the board, for a given p, then
;; - the row is (quotient p 9)
;; - the column is (remainder p 9)
;; ======================================
;; Constants:
(define B false) ;B stands for blank
(define BD1
(list B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B))
(define BD2
(list 1 2 3 4 5 6 7 8 9
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B
B B B B B B B B B))
(define BD3
(list 1 B B B B B B B B
2 B B B B B B B B
3 B B B B B B B B
4 B B B B B B B B
5 B B B B B B B B
6 B B B B B B B B
7 B B B B B B B B
8 B B B B B B B B
9 B B B B B B B B))
(define BD4 ;easy
(list 2 7 4 B 9 1 B B 5
1 B B 5 B B B 9 B
6 B B B B 3 2 8 B
B B 1 9 B B B B 8
B B 5 1 B B 6 B B
7 B B B 8 B B B 3
4 B 2 B B B B B 9
B B B B B B B 7 B
8 B B 3 4 9 B B B))
(define BD4s ;solution to 4
(list 2 7 4 8 9 1 3 6 5
1 3 8 5 2 6 4 9 7
6 5 9 4 7 3 2 8 1
3 2 1 9 6 4 7 5 8
9 8 5 1 3 7 6 4 2
7 4 6 2 8 5 9 1 3
4 6 2 7 5 8 1 3 9
5 9 3 6 1 2 8 7 4
8 1 7 3 4 9 5 2 6))
(define BD5 ;hard
(list 5 B B B B 4 B 7 B
B 1 B B 5 B 6 B B
B B 4 9 B B B B B
B 9 B B B 7 5 B B
1 8 B 2 B B B B B
B B B B B 6 B B B
B B 3 B B B B B 8
B 6 B B 8 B B B 9
B B 8 B 7 B B 3 1))
(define BD5s ;solution to 5
(list 5 3 9 1 6 4 8 7 2
8 1 2 7 5 3 6 9 4
6 7 4 9 2 8 3 1 5
2 9 6 4 1 7 5 8 3
1 8 7 2 3 5 9 4 6
3 4 5 8 9 6 1 2 7
9 2 3 5 4 1 7 6 8
7 6 1 3 8 2 4 5 9
4 5 8 6 7 9 2 3 1))
(define BD6 ;hardest ever? (Dr Arto Inkala)
(list B B 5 3 B B B B B
8 B B B B B B 2 B
B 7 B B 1 B 5 B B
4 B B B B 5 3 B B
B 1 B B 7 B B B 6
B B 3 2 B B B 8 B
B 6 B 5 B B B B 9
B B 4 B B B B 3 B
B B B B B 9 7 B B))
(define BD7 ; no solution
(list 1 2 3 4 5 6 7 8 B
B B B B B B B B 2
B B B B B B B B 3
B B B B B B B B 4
B B B B B B B B 5
B B B B B B B B 6
B B B B B B B B 7
B B B B B B B B 8
B B B B B B B B 9))
(define ROWS
(list (list 0 1 2 3 4 5 6 7 8)
(list 9 10 11 12 13 14 15 16 17)
(list 18 19 20 21 22 23 24 25 26)
(list 27 28 29 30 31 32 33 34 35)
(list 36 37 38 39 40 41 42 43 44)
(list 45 46 47 48 49 50 51 52 53)
(list 54 55 56 57 58 59 60 61 62)
(list 63 64 65 66 67 68 69 70 71)
(list 72 73 74 75 76 77 78 79 80)))
(define COLS
(list (list 0 9 18 27 36 45 54 63 72)
(list 1 10 19 28 37 46 55 64 73)
(list 2 11 20 29 38 47 56 65 74)
(list 3 12 21 30 39 48 57 66 75)
(list 4 13 22 31 40 49 58 67 76)
(list 5 14 23 32 41 50 59 68 77)
(list 6 15 24 33 42 51 60 69 78)
(list 7 16 25 34 43 52 61 70 79)
(list 8 17 26 35 44 53 62 71 80)))
(define BOXES
(list (list 0 1 2 9 10 11 18 19 20)
(list 3 4 5 12 13 14 21 22 23)
(list 6 7 8 15 16 17 24 25 26)
(list 27 28 29 36 37 38 45 46 47)
(list 30 31 32 39 40 41 48 49 50)
(list 33 34 35 42 43 44 51 52 53)
(list 54 55 56 63 64 65 72 73 74)
(list 57 58 59 66 67 68 75 76 77)
(list 60 61 62 69 70 71 78 79 80)))
(define UNITS (append ROWS COLS BOXES))
;; ======================================
;; Functions:
;; Board -> Board or false
;; produce a solution for bd; or false if bd is unsolvable
;; Assume: bd is valid
#;
(define (solve bd) false) ; stub
(check-expect (solve BD4) BD4s)
(check-expect (solve BD5) BD5s)
(check-expect (solve BD7) false)
(define (solve bd)
(local [(define (solve--bd bd)
(if (solved? bd)
bd
(solve--lobd (next-boards bd))))
(define (solve--lobd lobd)
(cond [(empty? lobd) false]
[else
(local [(define try (solve--bd (first lobd)))]
(if (not (false? try))
try
(solve--lobd (rest lobd))))]))]
(solve--bd bd)))
;; Board Pos -> Val or false
;; Produce value at given position on board.
(check-expect (read-square BD2 5) 6)
(check-expect (read-square BD3 63) 8)
(define (read-square bd p)
(list-ref bd p))
;; Board Pos Val -> Board
;; produce new board with val at given position
(check-expect (fill-square BD1 0 1)
(cons 1 (rest BD1)))
(define (fill-square bd p nv)
(append (take bd p)
(list nv)
(drop bd (add1 p))))
;; Board -> (listof Board)
;; produce list of valid next boards from board
;; finds first empty square, fills it with Natural[1, 9], keeps only valid boards
#;
(define (next-boards bd) empty) ; stub
(check-expect (next-boards (cons 1 (rest BD1)))
(list (cons 1 (cons 2 (rest (rest BD1))))
(cons 1 (cons 3 (rest (rest BD1))))
(cons 1 (cons 4 (rest (rest BD1))))
(cons 1 (cons 5 (rest (rest BD1))))
(cons 1 (cons 6 (rest (rest BD1))))
(cons 1 (cons 7 (rest (rest BD1))))
(cons 1 (cons 8 (rest (rest BD1))))
(cons 1 (cons 9 (rest (rest BD1))))))
(define (next-boards bd)
(keep-only-valid (fill-with-1-9 (find-blank bd) bd)))
;; Board -> Pos
;; produces the position of the first blank square
;; Assume: the board has at least one blank square
#;
(define (find-blank bd) 0) ; stub
(check-expect (find-blank BD1) 0)
(check-expect (find-blank (cons 2 (rest BD1))) 1)
(check-expect (find-blank (cons 2 (cons 4 (rest (rest BD1))))) 2)
(define (find-blank bd)
(cond [(empty? bd) (error "The board didn't have a blank space.")]
[else
(if (false? (first bd))
0
(+ 1 (find-blank (rest bd))))]))
;; Pos Board -> (listof Board)
;; produce 9 boards, with blank filled with Natural[1, 9]
#;
(define (fill-with-1-9 p bd) empty) ; stub
(check-expect (fill-with-1-9 0 BD1)
(list (cons 1 (rest BD1))
(cons 2 (rest BD1))
(cons 3 (rest BD1))
(cons 4 (rest BD1))
(cons 5 (rest BD1))
(cons 6 (rest BD1))
(cons 7 (rest BD1))
(cons 8 (rest BD1))
(cons 9 (rest BD1))))
(define (fill-with-1-9 p bd)
(local [(define (build-one n)
(fill-square bd p (+ n 1)))]
(build-list 9 build-one)))
;; (listof Board) -> (listof Board)
;; produce list containing only valid boards
#;
(define (keep-only-valid lobd) empty) ; stub
(check-expect (keep-only-valid (list (cons 1 (cons 1 (rest (rest BD1))))))
empty)
(define (keep-only-valid lobd)
(filter valid-board? lobd))
;; Board -> Boolean
;; produce true if board is valid, false otherwise
;; valid means no unit on the board has the same value twice; false otherwise
#;
(define (valid-board? bd) false)
(check-expect (valid-board? BD1) true)
(check-expect (valid-board? BD2) true)
(check-expect (valid-board? BD3) true)
(check-expect (valid-board? BD4) true)
(check-expect (valid-board? BD5) true)
(check-expect (valid-board? (cons 2 (rest BD2))) false)
(check-expect (valid-board? (cons 2 (rest BD3))) false)
(check-expect (valid-board? (fill-square BD4 1 6)) false)
(define (valid-board? bd)
(local [; Is true only if all the units are valid
(define (valid-units? lou)
(andmap valid-unit? lou))
; Gets the values from a unit keeping only the numbers and checks for duplicates.
; If there is a duplicate, this function returns false because it is not valid.
(define (valid-unit? u)
(no-duplicates?
(keep-only-values
(read-unit u))))
; Maps each position in a unit to its cooresponding value
(define (read-unit u)
(map read-pos u))
; Returns the value from a given position (used to map)
(define (read-pos p)
(read-square bd p))
; Only keeps the numbers in a unit by using filter
(define (keep-only-values lovf)
(filter number? lovf))
; Is true if the no duplicates
(define (no-duplicates? lov)
(cond [(empty? lov) true]
[else
(if (member (first lov) (rest lov))
false
(no-duplicates? (rest lov)))]))]
(valid-units? UNITS)))
;; Board -> Boolean
;; produce true if board is solved
;; Assume: board is valid, so it is solved if it is full
#;
(define (solved? bd) false) ; stub
(check-expect (solved? BD1) false)
(check-expect (solved? BD2) false)
(check-expect (solved? BD4s) true)
(define (solved? bd)
(andmap number? bd))