Binary Search Tree
As programmers one of our goals is to write code that is efficient. We want our code to run fast and use as little memory as possible. One way to do this is to use a data structures. In this case, we can use a binary search tree to search for a value faster.
Lists
Before we talk about binary search trees, let's take a look at a shortcut to creating lists in Racket.
; A list of numbers would be
(cons 1 (cons 2 (cons 3 empty)))
; This can be also created by using the list primitive
(list 1 2 3)
These two lists are the same, it is just that the second one is easier to read and write.
(list 1 2 3)
; Lets say we want to add 4 to the list
(cons 4 (list 1 2 3))
; We can also add the contents of two lists together
(append (list 1 2 3) (list 4 5 6)) ; => (list 1 2 3 4 5 6)
Do note that we use cons to add a value to the list. This is because (cons 4 (list 1 2 3)) will give us a (list 4 1 2 3). However, if we do (list 4 (list 1 2 3)) we get a list of two elements not a list of 4 elements. The first element in the list is 4 and the second element is a list of 3 elements. Lists can have lists as elements.
Searching
Let's define a data definition for a bank account and a function that searches for a bank account with a given account number.
(define-struct account (num name))
; Accounts is one of:
; - empty
; - (cons (make-account Natural String) Accounts)
; interp. a list of accounts, where each
; num is an account number
; name is the person's first name
(define ACS1 empty)
(define ACS2 (list (make-account 1 "abc")
(make-account 4 "dcj")
(make-account 3 "ilk")
(make-account 7 "ruf")))
#;
(define (fn-for-accounts accs)
(cond [(empty? accs) (...)]
[else
(... (account-num (first accs)) ; Natural
(account-name (first accs)) ; String
(fn-for-accounts (rest accs)))]))
; Template rules used:
; - one of: 2 cases
; - atomic distinct: empty
; - compound: (cons (make-account Natural String) Accounts)
;; Accounts Natural -> String or false
;; Try to find account with given number in accounts. If found produce name, otherwise produce false.
#;
(define (lookup accs n) "") ; stub
(check-expect (lookup empty 2) false)
(check-expect (lookup (list (make-account 1 "abc")
(make-account 4 "dcj")) 1) "abc")
(check-expect (lookup (list (make-account 1 "abc")
(make-account 4 "dcj")) 4) "dcj")
(check-expect (lookup (list (make-account 1 "abc")
(make-account 4 "dcj")) 3) false)
(define (lookup accs n)
(cond [(empty? accs) false]
[else
(if (= (account-num (first accs)) n)
(account-name (first accs))
(lookup (rest accs) n))]))
This function works and will find the account with the given account number. However, it is really slow when the number of accounts we have is large. In the best case scenario, the account we are looking for is the first account in the list and the worst case is that it doesn't exist. If it doesn't exist we have to go through the entire list to find out that it doesn't exist. The other issue on average we have to go through half the list to find the account we are looking for. Let's say we have 1,000,000 accounts, we would have to go through 500,000 accounts on average to find the account we are looking for. This is not very efficient.
Binary Search Tree
A binary search tree had nodes and branches. Each node has a value and two branches. The left branch contains values that are less than the value of the node and the right branch contains values that are greater than the value of the node. The branches can be empty.
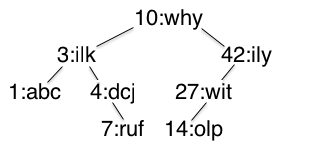
To be able to replicate the figure in code, we need to define a data definition for a binary search tree.
(define-struct node (key val l r))
;; A BST (Binary Search Tree) is one of:
;; - false
;; - (make-node Integer String BST BST)
;; interp. false means no BST, or empty BST
;; key is the node key
;; val is the node val
;; l and r are left and right subtrees
;; INVARIANT: for a given node:
;; key is > all keys in its l(eft) child
;; key is < all keys in its r(ight) child
;; the same key never appears twice in the tree
This binary tree takes self references twice in order to create the left and right branches. This is because each branch is a smaller binary search tree. Also note that there are invariant rules that must be followed for this data definition to be valid. The key of the node must be greater than all the keys in the left branch and less than all the keys in the right branch. Also, the same key cannot appear twice in the tree.
(define BST0 false)
(define BST1 (make-node 1 "abc" false false))
(define BST4 (make-node 4 "dcj" false (make-node 7 "ruf" false false)))
(define BST3 (make-node 3 "ilk" BST1 BST4))
(define BST42
(make-node 42 "ily"
(make-node 27 "wit" (make-node 14 "olp" false false) false)
false))
; This is the same as figure 1
(define BST10 (make-node 10 "why" BST3 BST42))
Faster Searching
Now that we have a binary search tree, we can create a faster function to search. If the value of the node is the value we are looking for, we can return the value. If the value of the node is greater than the value we are looking for, we can search the left branch. If the value of the node is less than the value we are looking for, we can search the right branch. If we reach a false, we know that the value we are looking for does not exist in the tree.
; BST Natural -> String or false
; Try to find node with given key, if found produce value; if not found produce false.
#;
(define (lookup-key t k) "") ; stub
(check-expect (lookup-key BST0 99) false)
(check-expect (lookup-key BST1 1) "abc")
(check-expect (lookup-key BST1 0) false) ; L fail
(check-expect (lookup-key BST1 99) false) ; R fail
(check-expect (lookup-key BST10 1) "abc") ; L L succeed
(check-expect (lookup-key BST10 4) "dcj") ; L R succeed
(check-expect (lookup-key BST10 27) "wit") ; R L succeed
(check-expect (lookup-key BST10 50) "dug") ; R R succeed
(define (lookup-key t k)
(cond [(false? t) false]
[else
(cond [(= k (node-key t))
(node-val t)]
[(< k (node-key t)) ; should we go left
(lookup-key (node-l t) k)]
[(> k (node-key t)) ; should we go right
(lookup-key (node-r t) k)])]))
Now the question is how fast is this function at searching? This on average takes log n time to search so for 1,000,000 accounts, it would take 20 steps to find the account we are looking for. This is much faster than the previous function which took 500,000 steps on average on the same data.